Capacitor

A capacitor is an electrical device that consists of two conductors with a dielectric in between. The most popular type is the parallel-plate capacitor. Capacitors integrate the input current signal and differentiate the input voltage. Capacitors build up charge (functioning as a storage device) when placed in an electric circuit, most commonly AC circuits or transient circuits (first- or second-order). Stored charge is governed by:

$$q=CV$$

where the constant $C$ is the capacitance, measured in farads ($F$, coulombs per volts). The capacitance depends only on the geometry of the capacitor’s plates and not on its charge or potential difference.

Circuit analysis

The governing equations for a capacitor are:

$$i=C\frac{dv}{dt}$$ $$v(t)=v(t_0)+\frac{1}{C}{\int }_{t_0}^{t}i(\tau )d\tau$$

The impedance is given by:

$$Z_C=\frac{1}{j\omega C}=-\frac{j}{\omega C}$$

In the Laplace domain:

$$I(s)=CsV(s)-Cv(0^{-})$$ $$V(s)=\frac{1}{Cs}I(s)+\frac{v(0^{-})}{s}$$

The instantaneous and average power is given by:

$$p(t)=-\frac{\omega C{V}_A^2}{2}\sin (2\omega t)$$ $$P=0$$

The energy stored by a capacitor is given by:

$$W_e=\frac{1}{2}C{V}^2$$

Equivalence

For capacitors connected in parallel:

$$C_{eq}=\sum _{j=1}^n{C}_j$$

For capacitors connected in series:

$$\frac{1}{C_{eq}}=\sum _{j=1}^n\frac{1}{C_j}$$

Behaviour

A fully charged capacitor will match the voltage of a battery if in series with the battery.

From the impedance formula, we observe that high frequencies will result in lower impedance. And lower frequencies will result in a higher impedance. At the lowest possible frequency (DC conditions), it’ll act effectively as an open circuit.

Capacitors are also divided into polar and non-polar types. In general, polar capacitors use an electrolyte as a dielectric and have positive/negative terminals. For small-signal or AC applications, we prefer using non-polar capacitors since they don’t get damaged for signals of varying polarity.

Electromagnetism

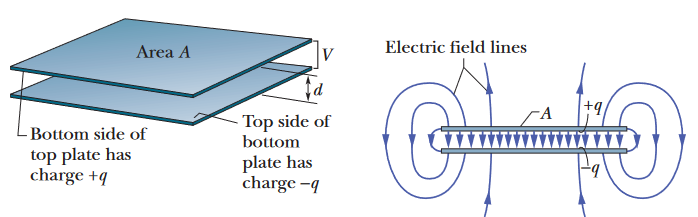
Because the plates are conductors, they are equipotential surfaces — and all points on a plate are at the same electric potential; we represent the potential difference with $V$. When they are uncharged, $V=0$.

Note that $\kappa$ is the dielectric constant of the material between the plates. ${\kappa }_{\text{air}}=1$.

$$C=\kappa C_{\text{air}}$$

Why do we have a dielectric? This prevents current flow or leakage. Capacitance is independent of an increase in one of the parameters. If the charge increases, so too will the electric field, and the voltage. So the overall increase will cancel out.

Capacitors can also act as resistors:

$$C=\frac{\oint {\oint }_Sϵ\vec{E}\cdot d\vec{s}}{{\int }_{+}^{-}\vec{E}\cdot d\vec{l}}$$ $$R=\frac{{\int }_{+}^{-}\vec{E}\cdot d\vec{l}}{{\iint }_S\sigma \vec{E}\cdot d\vec{s}}$$

If $ϵ,\sigma$ are constant, then we get:

$$CR=\frac{ϵ}{\sigma }$$

Computations

Occasionally we’re asked to find the capacitance:

$$C=\frac{q}{v}$$

There are two ways to approach this. Under method 1, we set an arbitrary $q$ and find $\vec{E}$ with Gauss’ law.

$$V={\int }_a^b\vec{E}\cdot d\vec{l}$$

Where points $a,b$ are arbitrary. Then, we can find the capacitance by dividing $q$ by our expression for $V$. The arbitrary $q$ (that is unknown and we set in the beginning) will cancel out in the end.

Under method 2, we set the voltage and find $\vec{E}$ or $\vec{D}$, with Poisson’s equation (or Laplace’s equation if the medium is uniform $[ϵ=0]$ and there is no ${\rho }_v$).

We find $V$, then:

$$\vec{E}=-\nabla V$$ $$\vec{D}=ϵ\vec{E}$$

Once we find $\vec{E}$, we can find $\vec{D}$, and find ${\rho }_s$ with a boundary condition:

$$\hat{n}\cdot ({\vec{D}}_2-{\vec{D}}_1)={\rho }_s$$

Since one will probably be grounded, it makes sense to set one of the $\vec{D}$ to $\vec{0}$. With ${\rho }_s$, we integrate to find $q$.

Then when we substitute into the expression for the capacitance, the $V_0$ cancels out.

Simple geometry

For a parallel-plate capacitor, where $\kappa$ is the dielectric constant of the material between the plates:

$$C=\frac{\kappa {ϵ}_{0}A}{d}$$ $$V=\frac{Qd}{A{ϵ}_0}$$ $$E=\frac{Q}{A{ϵ}_0}$$

For a cylindrical capacitor, where $a,b$ are the respective radii of the extremities:

$$C=\frac{2\pi {ϵ}_{0}L}{\ln (\frac{b}{a})}$$

For a spherical capacitor:

$$C=4\pi {ϵ}_0\frac{ab}{b-a}$$

For an isolated sphere of radius $R$:

$$C=4\pi {ϵ}_{0}R$$

See also

• Inductor