RLC circuit

RLC circuits (or alternatively second-order transient circuits) are dynamic circuits with a resistor, capacitor, and inductor as elements. They’re described with second-order ODEs, specifically linear ODEs with constant coefficients.

Two important cases are the series RLC circuit, and the parallel RLC circuit.

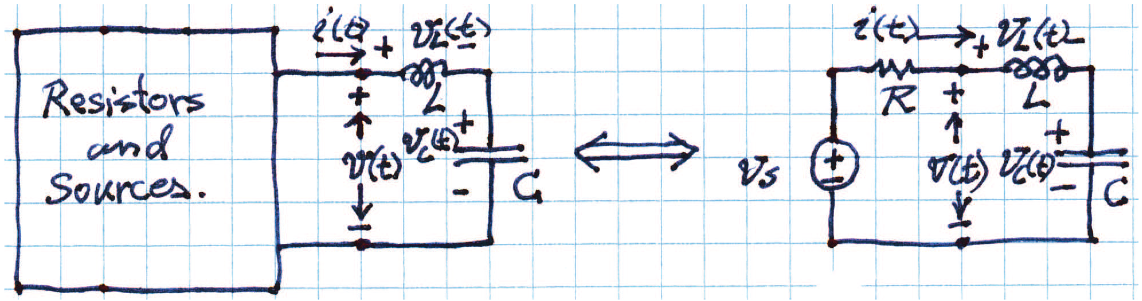
Series circuit

The series circuit is the easiest to derive. Using KVL around the loop, we have:

$$v_L(t)+v_R(t)+v_C(t)=v_s(t)$$

We have either two options. We can represent in terms of charge (which we do in ODE classes) or in terms of the capacitor voltage (which we do in circuit classes). Both are the same, since $v_c=\frac{q}{C}$, but our final result will be different because we look for a different variable.

$$LC{v}_c^{\prime \prime }+RC{v}_c^{\prime }+v_c(t)=v_s(t)$$ $$L{q}^{\prime \prime }+R{q}^{\prime }+\frac{1}{C}q=E(t)$$

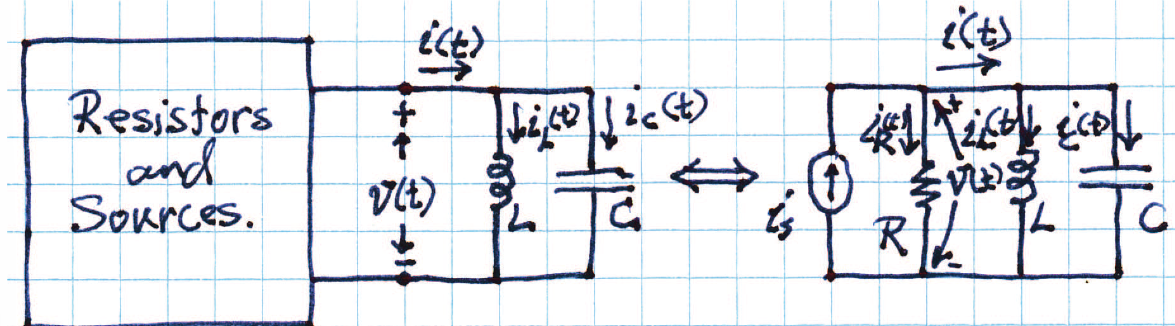
Parallel circuit

The parallel circuit uses KCL at the top node, which gets us:

$$i_c(t)+i_R(t)+i_L(t)=i_s(t)$$

We take the inductor current as our function to solve for.

$$LC{i}_L^{\prime \prime }+\frac{L}{R}{i}_L^{\prime }+i_L(t)=i_s(t)$$

Additional notes

The zero-input circuit (or natural-response circuit) is where $v_s(t)$ is set to 0 for all $t$, i.e., it has been shorted. The natural frequency and damping ratio are given by:

$${\omega }_0=\frac{1}{\sqrt{LC}}$$ $$\zeta =\frac{R}{2}\sqrt{\frac{C}{L}}$$