Voltage

The electric potential ($V$) is the work done by an electric field of a charged object to bring a positive test charge $q_0$ from an infinite distance to a point $P$. It’s measured in volts (V).

$$V=\frac{-W_{\infty }}{q_0}=\frac{U}{q_0}=\frac{dw}{dq}$$

where $W_{\infty }$ is the work done, and $U$ is the electric potential energy that would then be stored in the system. Potential is a scalar quantity. Unlike the electric field, it does not follow direct superposition (i.e., we can’t necessarily go around cancelling things out because it’s not a vector).

Circuit analysis

Voltage drops over components in series according to Ohm’s law, $v=iR$. Components in parallel with each other all have the same voltage.

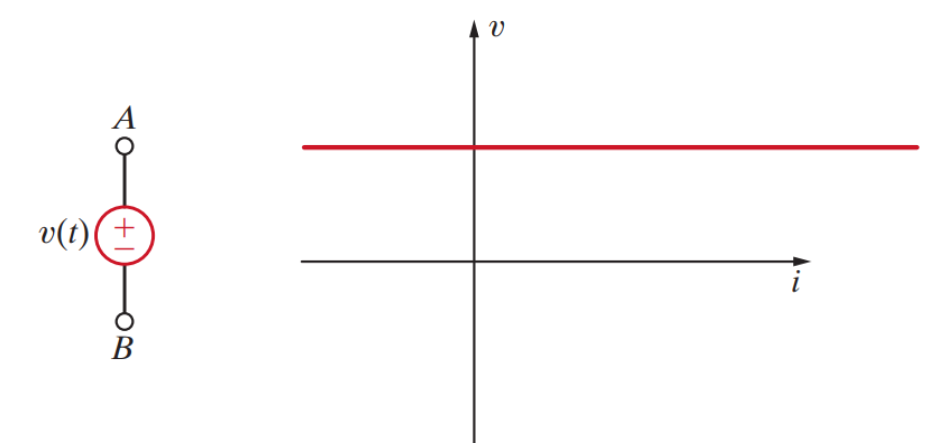
Independent voltage sources maintain a specified voltage.

The voltage transfer characteristic (VTC) of a circuit is a plot of its output voltage against its input voltage. This reveals some important insights into the operation of an amplifier circuit. For instance, for a MOSFET amplifier, the output is $v_{GS}$ and input $v_{DS}$. For a BJT, the output is $v_{CE}$ and input $v_{BE}$.

Electromagnetism

Static conditions

The potential difference (or just voltage) is the work per unit charge against an electric field to move an object from two points $P_1\to P_2$. This is path independent, i.e., we can integrate along any contour between the points.

$$V_{21}=V_2-V_1=-{\int }_{P_1}^{P_2}\vec{E}\cdot d\vec{l}$$

Importantly, under electrostatic conditions, the integral over a closed contour (i.e., path starting and ending at the same point) is zero (similarly to KVL):

$${\oint }_C\vec{E}\cdot d\vec{l}=0$$

We can also express in terms of the electric field, where $\nabla$ is the gradient operator. This allows us to avoid using Coulomb’s law to find the field:

$$\vec{E}=-\nabla V$$

When doing computations for the potential difference, we want to split our contour into the one that is the most convenient because of the path independence of electrostatic fields. Because of the dot product, we always want to work perpendicular or parallel to the field.

Depending on the geometry, we sometimes can’t set a reference point at $\infty$. Instead, we take the reference point at a finite distance away from the charge distribution.

When can we use $\infty$?

We can take $\infty$ as a reference point for a finite charge distribution. For example, a charged ring, or a charged plane/sphere with finite dimensions are distributions we can. An infinite line charge is one that we can’t.

What do we do then? We can use Poisson’s equation or Laplace’s equation and set up a boundary-value problem for the potential.

Where does the physical intuition come from? If we rewrite the integral above:

$$-{\int }_{P_1}^{P_2}\vec{E}\cdot d\vec{l}=-\frac{1}{q}{\int }_{P_1}^{P_2}q\vec{E}\cdot d\vec{l}=-\frac{1}{q}{\int }_{P_1}^{P_2}\vec{F}\cdot d\vec{l}$$

In plain text, this corresponds with our definition above.

Dynamic conditions

In electrodynamic conditions, the voltage produced by Faraday’s law is called the electromotive force. This has a few implications