Line integral

Line integrals (or also sometimes contour integrals) are one dimensional integrals of either scalar functions or vector fields along curves. They’re motivated by the idea that in higher dimensions, we integrate over a region but we might still need the area under a curve.

Important extensions of line integrals are:

• Contour integral, in complex analysis
• Flux
• Circulation

Scalar functions

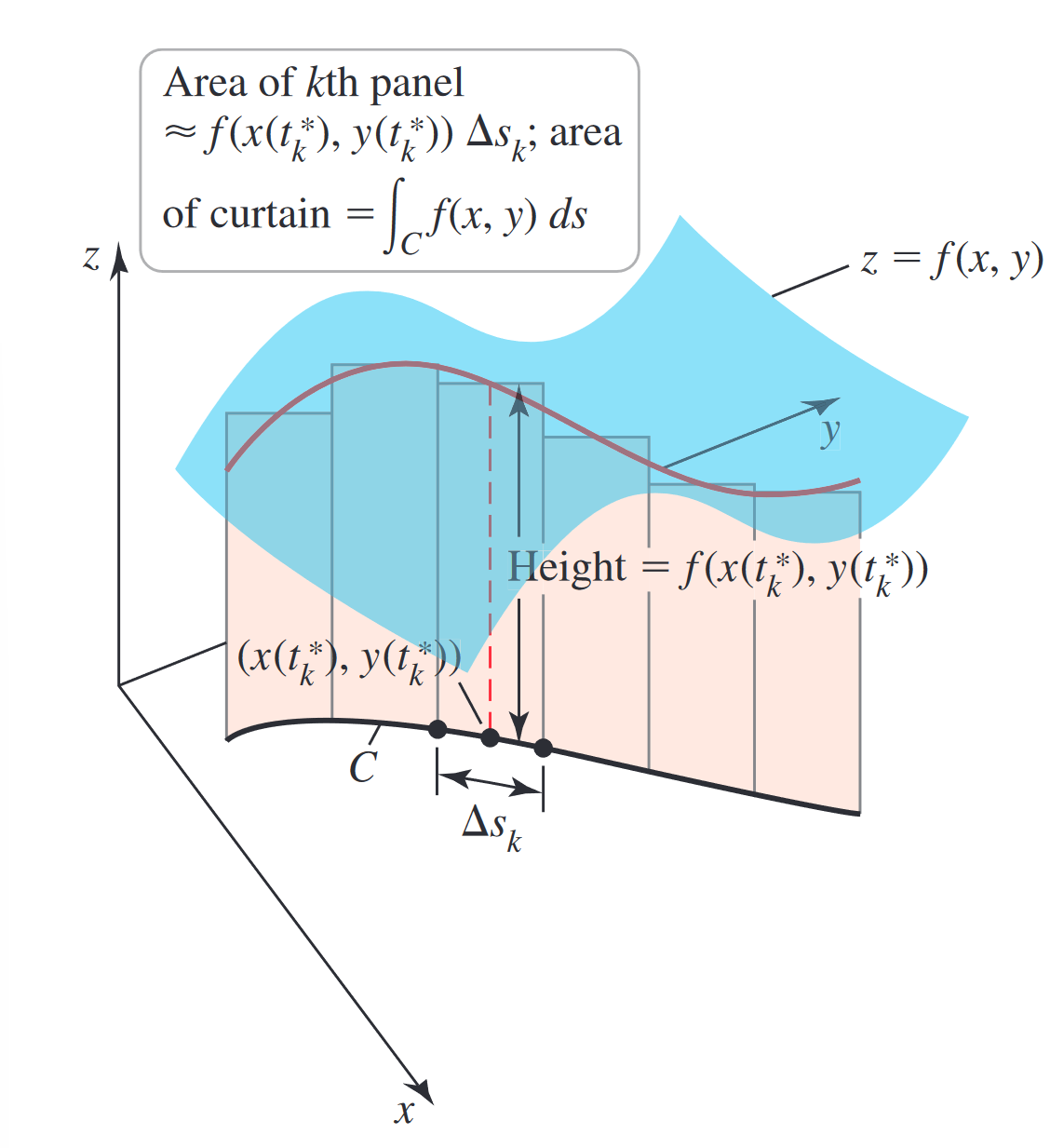
An introductory case involves the integration of a scalar function $f$ over a curve. The steps are pretty simple:

$${\int }_{C}fds={\int }_a^{b}f(x(t),y(t))|{\vec{r}}^{\prime }(t)|dt$$

We must parameterise $C$ in the form $\vec{r}(t)=⟨x(t),y(t)⟩$ within some interval of $t$. Then, we say that:

$$ds=|{\vec{r}}^{\prime }(t)|dt=\sqrt{x^{\prime }(t{)}^2+y^{\prime }(t{)}^2}dt$$

And substitute back in. This is still applicable for ${\mathbb{R}}^3$ as well.

Foundations

Line integrals are formulated from Riemann sums similar to other integrals. The idea is that we take the 2-dimensional area underneath the curve, i.e., differently from what arc-length does.

See also

• Surface integral, the double integral equivalent
• Stokes’ theorem