Riemann sum

Riemann sums suppose that we can approximate the definite integral of functions with some number of rectangles. As we increase the number of rectangles we increasingly get a better approximation, such that:

$${\int }_a^{b}f(x)dx=\underset{n\to \infty }{\lim }\sum _{k=0}^{n-1}f(x_k^{\ast })\Delta x=\underset{n\to \infty }{\lim }\sum _{k=1}^{n}f(x_k^{\ast })\Delta x$$

Where the first is a left-endpoint Riemann sum and the second is a right-endpoint Riemann sum. Midpoint sums can use either. Our representative point $x_k^{\ast }$ will also change depending on what type we use:

$$L_n:x_k^{\ast }=x_0+(k-1)\Delta x$$ $$R_n:x_k^{\ast }=x_0+k\Delta x$$ $$M_n:x_k^{\ast }=x_0+(k-\frac{1}{2})\Delta x$$

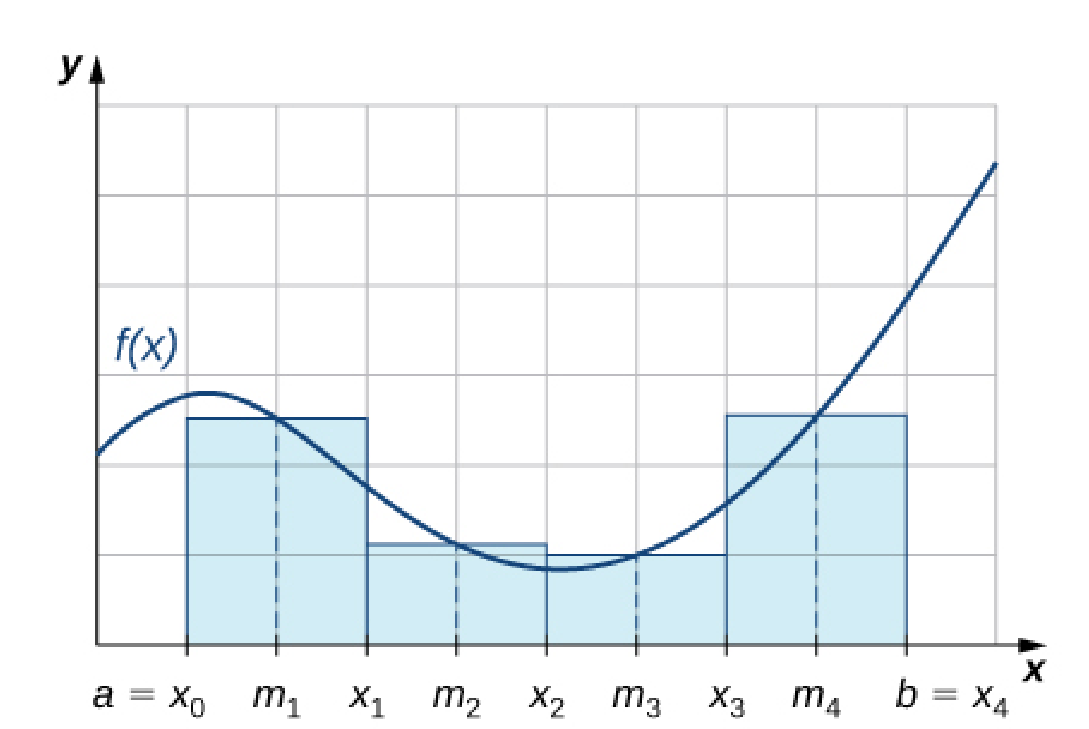
The below shows the midpoint rule.¹ The idea of a Riemann sum also aids us in multivariable integration, particularly with double and triple integrals.

See also

• Trapezium rule

Footnotes

1. From Calculus 2 by Gilbert Strang. ↩