Double integral

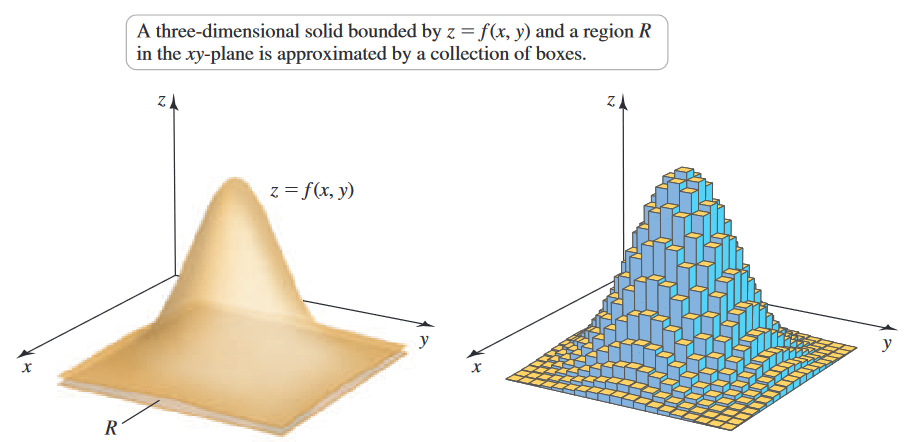
We extend from the idea of single-variable calculus, where the infinitesimally small quantity is length, to double integrals, where the differential element is of area. They’re commonly used to calculate volume (though sometimes area).

$${\iint }_{R}f(x,y)dA=\underset{n\to \infty }{\lim }\sum _{k=1}^{n}f(x_k^{\ast },y_k^{\ast })\Delta A_k$$

For rectangular regions, very importantly, Fubini’s theorem for double integrals tells us that:

$${\iint }_{R}f(x,y)dA={\int }_c^d{\int }_a^{b}f(x,y)dxdy={\int }_a^b{\int }_c^{d}f(x,y)dydx$$

What this means is that we can compute two separate single integrals, just holding the other variable constant. The first single integral we evaluate with respect to is the first differential element. As a key result, we should choose the easiest integral to evaluate first.

When $f=1$, we discuss area. Note that we also computed area with single integrals, but it was the net signed area. With double integrals, we avoid this mess altogether.

General regions

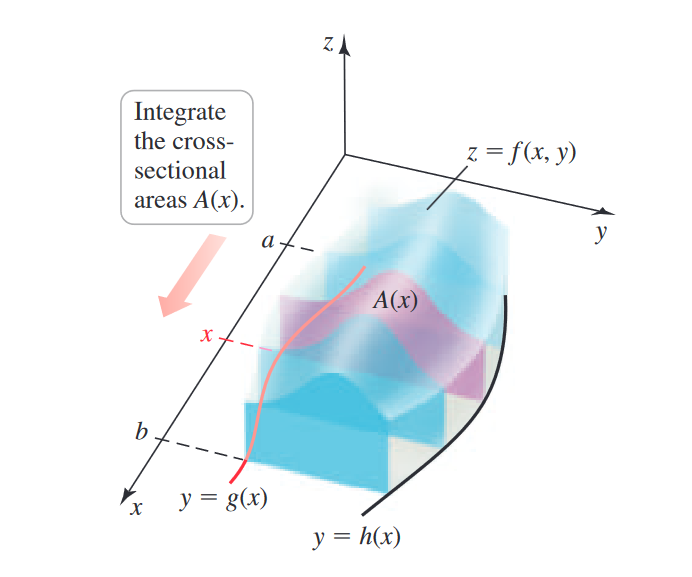
However! We may not have rectangular regions, and instead general regions, i.e., consider where the region is bounded by two functions. If $R$ is bounded above and below by the continuous functions $y=g(x)$ and $y=h(x)$ and the lines $x=a$ and $x=b$, then:

$${\iint }_{R}f(x,y)dA={\int }_a^b{\int }_{g(x)}^{h(x)}f(x,y)dydx$$

Similar to single integration, where we can swap the variable we are integrating over, we can similarly integrate in terms of a function $y$.

$${\iint }_{R}f(x,y)dA={\int }_a^b{\int }_{g(y)}^{h(y)}f(x,y)dxdy$$

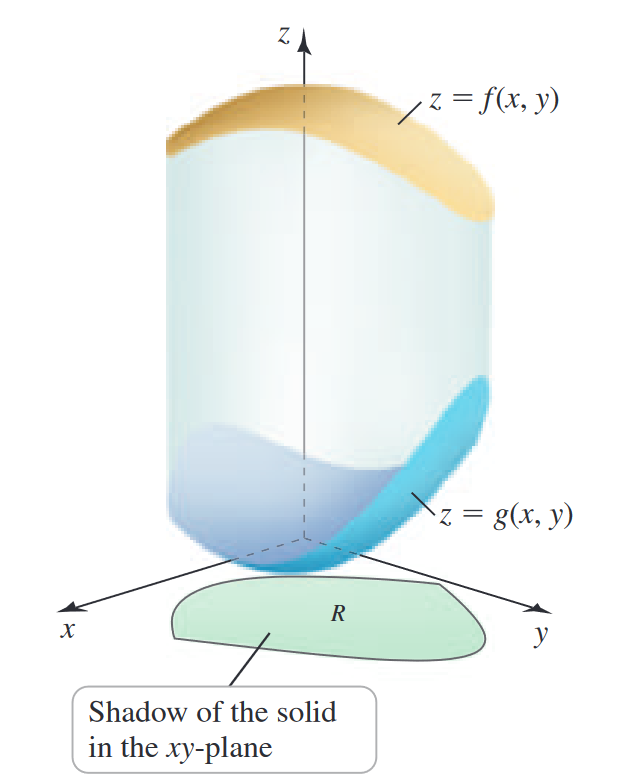
Either way, the same philosophy above holds true. In choosing our order of integration, we choose what is easier to perform first. We can also compute the volume between bounding surfaces (like how with single integrals we can calculate the area between bounding lines), we have:

$$V={\iint }_{R}f(x,y)dA-{\iint }_{R}g(x,y)dA$$

Additionally, where one of the upper or lower boundaries for the regions may not be continuously differentiable, then we can decompose the integral into the sum of separate sub-regions.

Applications, special cases

The average value of a function over a plane region $R$ is:

$$\bar{f}=\frac{1}{\text{area of R}}{\iint }_{R}f(x,y)dA=\frac{{\iint }_{R}f(x,y)dA}{{\iint }_{R}dA}$$

Additionally, when we discuss even functions ($f(x)=f(-x)$) or odd functions ($f(-x)=-f(x)$), we have a useful symmetrical property that reduces computation time. Recall from single integration that for an odd function and even function, respectively:

$${\int }_{-a}^{a}f(x)dx=0$$ $${\int }_{-a}^{a}f(x)dx=2{\int }_0^{a}f(x)dx$$

It turns out that a similar property holds true for double integrals. If $f(-x,-y)=-f(x,y)$, then:

$${\iint }_{R}f(x,y)dA=0$$ $${\iint }_{R}f(x,y)dA=2$$

Addendums

Just as with single integrals, we can build up with a Riemann sum:

See also

• Triple integral