Dirac delta function

The Dirac delta function (also impulse function and delta function) is characterised by the properties:

$$\delta (t-t_0)=\{\begin{array}{ll}\infty & t=t_0\\ 0& t\ne t_0\end{array}$$ $${\int }_{-\infty }^{\infty }\delta (t-t_0)dt=1$$ $${\int }_{-\infty }^{t_0}\delta (t-t_0)dt={\int }_{t_0}^{\infty }\delta (t-t_0)dt=\frac{1}{2}$$

Uniquely, the delta function has a sifting property that allows it to sample at a given $t=t_0$.

$${\int }_{-\infty }^{\infty }f(t)\delta (t-t_0)dt=f(t_0)$$ $$\sum _{n=-\infty }^{\infty }x[n]\delta [n-n_0]=x[n_0]$$

Signal theory

The Laplace transform is given by:

$$\mathcal{L}\{\delta (t-t_0)\}=e^{-s{t}_0}$$

The study of a system’s impulse response is a key application of the delta function.

The discrete-time unit impulse $\delta [n]$ is defined the same way the CT delta function is defined, except at $n=t_0$, we have $\delta =1$. This is called the Kronecker delta function. 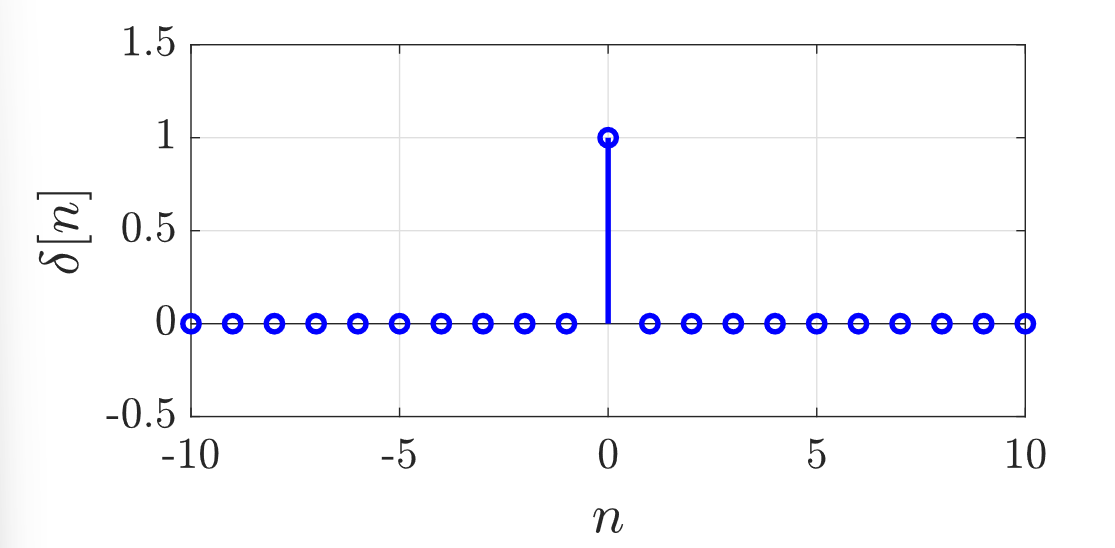This is mostly useful for defining DT signals at specific points, but we can also define any DT signal with a sum of individual impulses.

$$\delta [n]=u[n]-u[n-1]$$ $$u[n]=\sum _{n=0}^{\infty }\delta [n]$$

Similar to the continuous-time case, we have a sifting formula, which essentially samples the signal at a specific point $n_0\in \mathbb{Z}$:

$$x[n_0]=\sum _{n=-\infty }^{\infty }x[n]\delta [n-n_0]$$

Curiously:

$$\delta (t)=\frac{d}{dt}u(t)$$ $$u(t)={\int }_{-\infty }^t\delta (\tau )d\tau$$

i.e., for differentiation in the CT case, we have a difference in the DT case.

Occasionally we will get expressions of a modified impulse train, like follows:

$$x[n]=\sum _{m=-\infty }^{\infty }(-1{)}^m(\delta [n-2m]+\delta [n+3m])$$

What do we do here? The trick is to ignore the $n$ and focus in on the $m$ terms. Draw out the $m$ terms spaced out as specified in the equation.

The delta function is also a uniform superposition of all frequency components:

$$\delta (t-t_0)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{e}^{i\omega (t-t_0)}d\omega$$

Electromagnetism

Because of the nature of the delta function, we can use it to model the behaviour of a scalar or vector-valued function that is infinite or undefined at certain points and zero elsewhere. If there’s thickness, then we don’t use the delta function.

How do we know when to use the delta function?

Some cases:

• If something is infinitely thin.
• If there’s a “shell” with an infinitesimally small thickness.

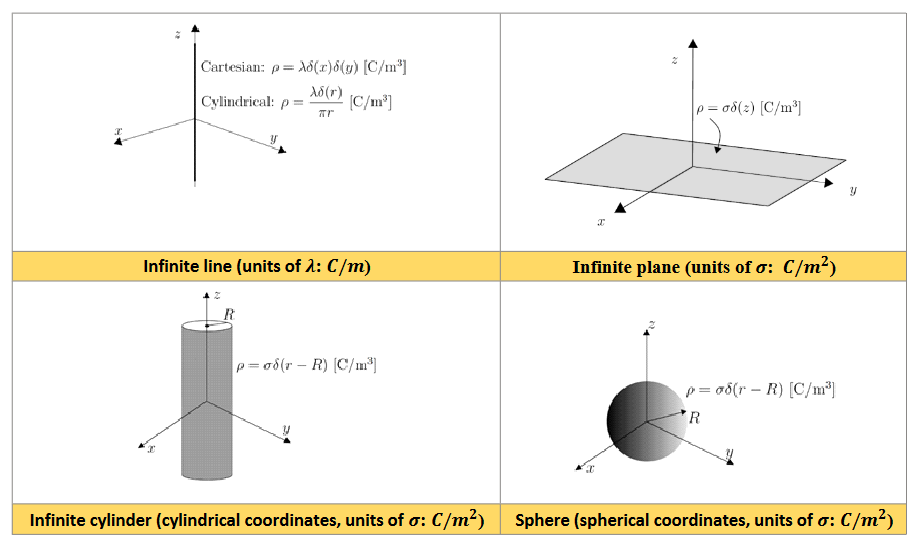
Scalar density is given by:

• Volume distribution, by $\rho$.
• Surface distribution, by $\sigma$.
• Line distribution, by $\lambda$.
• Point charge, by $Q$.

Common geometries take the form below. I like to think about it as the delta function being of a variable that is essentially perpendicular to the geometry (see the line for an example).

Across a surface

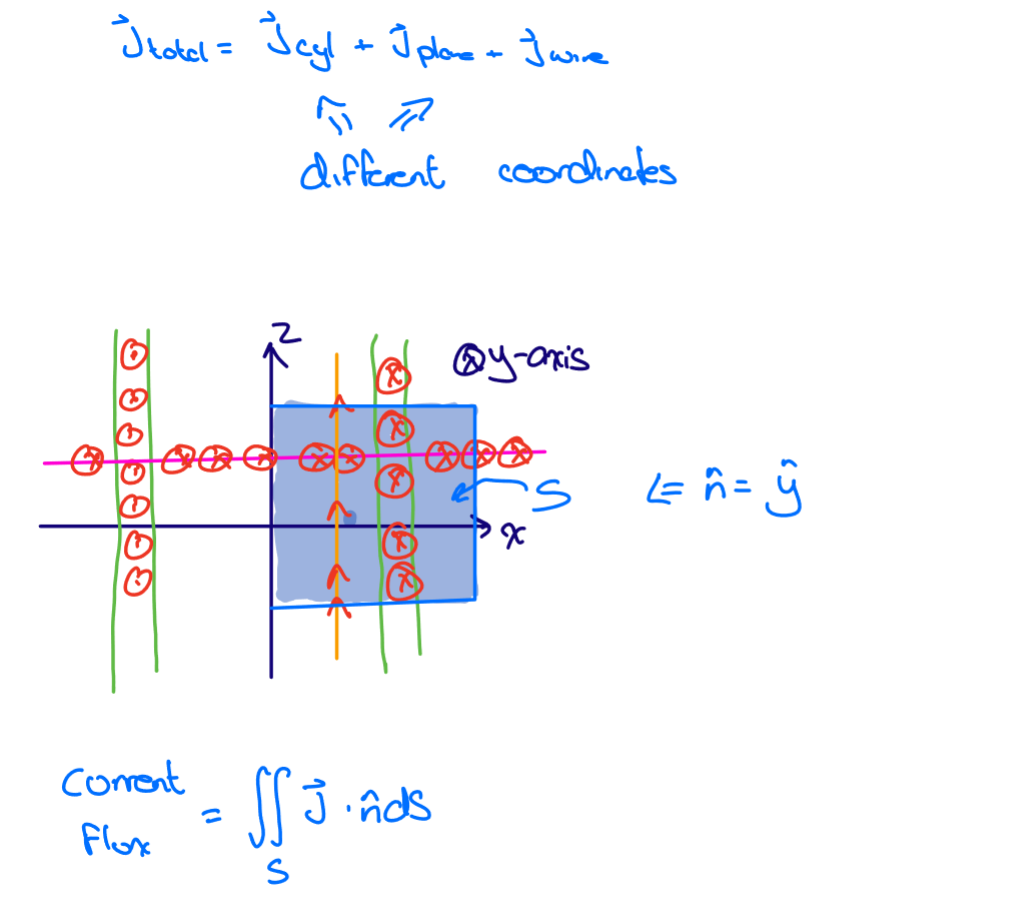
Many practice questions take the form below. Let’s decompose what’s going on: Immediately what we notice:

• The cylindrical shell cannot be approximated with the delta function because it has some thickness. We express with the $\theta$ unit vector because of its given orientation.
• The plane and wire must be approximated with the delta function.
• The normal vector is perpendicular to the surface, i.e., $\hat{n}=\hat{y}$.
• The surface bounds are given: these are the surface integral bounds.

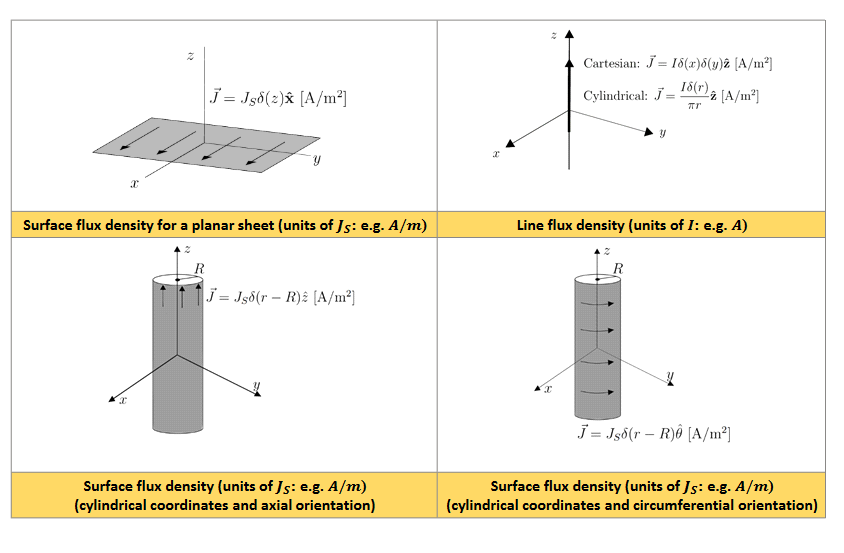
I think the idea behind converting from rectangular to cylindrical/spherical is that we don’t want more than one delta function in the integrand.

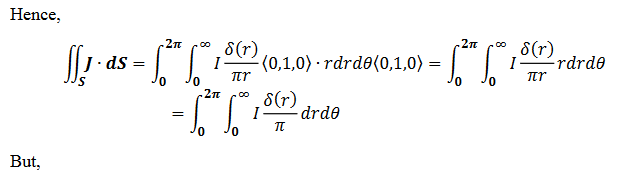
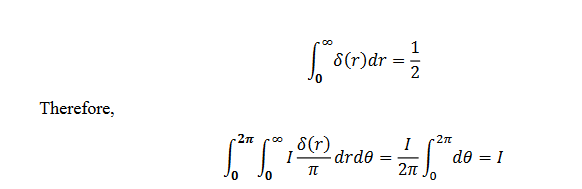
Motivations

In electrical engineering, systems are sometimes acted upon by an emf of a large magnitude for only a short amount of time. A similar case is true for mechanical systems with forces. Think about lightning, or a baseball bat hitting a ball.

The delta function approximates a piecewise-defined function defined by:

$$p_{\Delta }(t-t_0)=\{\begin{array}{ll}0& 0\le t<t_0-a\\ \frac{1}{2a}& t_0-a\le t<t_0+a\\ 0& t\ge t_0+a\end{array}$$

i.e., the continuous-time unit pulse. We observe that the area under the unit pulse is:

$${\int }_{-\infty }^{\infty }{p}_{\Delta }(t)dt=1$$

The Dirac delta function is in turn defined by the limit:

$$\delta (t-t_0)=\underset{a\to 0}{\lim }{p}_{\Delta }(t-t_0)$$

There isn’t a function that actually satisfies the properties above — the delta function is a distribution. The delta function is only meaningful in the context of an integral. We can’t manipulate it like a regular function (i.e., ${\delta }^2(t)$ is meaningless). An alternative definition of the delta function involves the normal distribution:

$$\delta (t)=\underset{a\to 0}{\lim }\frac{1}{a\sqrt{\pi }}{e}^{-(\frac{x}{a}{)}^2}$$

As $a$ approaches 0, then the distribution looks more and more like the delta function. This also allows it to satisfy the integral properties (area is 1).

In programming

In MATLAB, we can define the Dirac delta function:

syms a, t
f = dirac(t - a)