Sampling

In signal processing, sampling is the act of taking regular and periodic values of a continuous-time signal to create a discrete-time signal. The opposite conversion, from a DT signal to a CT signal is interpolation. Where $T_s$ is defined as the sampling period:

$$x_s[n]=x(t){|}_{t=n{T}_s}=x(n{T}_s)$$

The sampling function is defined as:

$$s(t)=\sum _{n=-\infty }^{\infty }\delta (t-n{T}_s)$$

i.e., we have an infinite CT impulse train spaced out by $T_s$ seconds. Then, when we sample a function $x$, we multiply to get a periodic weighted sum of impulses:

$$s(t)x(t)=\sum _{n=-\infty }^{\infty }\delta (t-n{T}_s)x(t)=\sum _{n=-\infty }^{\infty }\delta (t-n{T}_s)x(n{T}_s)$$

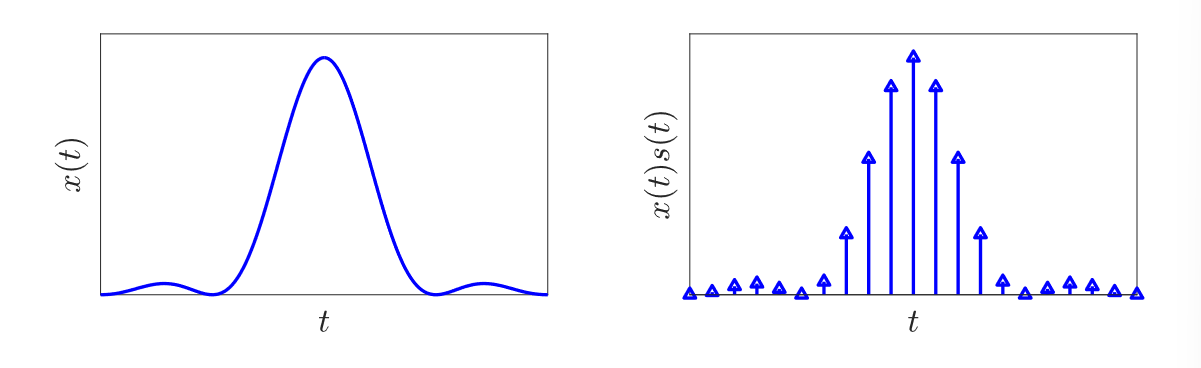Some common sampling rates: audio (at 44 100 samples per second) or video (at 30 samples per second). Our key questions with sampling involve the following, both of which are answered with the Nyquist-Shannon theorem for a bandlimited signal:

• How small should $T_s$ be?
• How can we reconstruct the original CT signal $x(t)$ from the DT samples $x[n]$?

Fourier series

Since the sampling function is periodic, we can take the CTFS. The CTFS coefficients are given by (where ${\omega }_s$ is the fundamental angular frequency of $s$):

$${\alpha }_k=\frac{1}{T_s}\sum _{n=-\infty }^{\infty }{\int }_{-\frac{T_s}{2}}^{\frac{T_s}{2}}\delta (t-n{T}_s)e^{-jk{\omega }_{s}t}dt$$

Since we have a bounded interval, and because of the nature of the delta function, the integrand is only zero if $n\ne 0$ and equal to 1 for $n=0$. So the coefficient reduces to:

$${\alpha }_k=\frac{1}{T_s}$$ $$s(t)=\frac{1}{T_s}\sum _{k=-\infty }^{\infty }{e}^{jk{\omega }_{s}t}$$

Since the coefficients represent the strength of the harmonic frequencies present in the signal, we observe that the CTFT spectrum has equal contributions from all harmonics.

$$S(j\omega )=\frac{2\pi }{T_s}\sum _{k=-\infty }^{\infty }\delta (\omega -k{\omega }_s)$$

i.e., the CTFT of the sampling function is itself a periodic sampling function with period ${\omega }_s$.¹

Footnotes

1. Prof Pavel called this the “picket fence miracle”. ↩