Continuous-time Fourier series

The continuous-time Fourier series (CTFS) expresses a periodic continuous-time signal as the weighted sum of sinusoids whose frequencies are related. See also the discrete-time equivalent.

For a periodic function that is neither even nor odd, we use the continuous-time Fourier series:

$$\hat{x}(t)=\sum _{k=-K}^K{a}_k{e}^{jk{\omega }_{0}t};a_k\in \mathbb{C}$$ $${\alpha }_k=\frac{1}{T_0}{\int }_0^{T_0}x(t)e^{-jk{\omega }_{0}t}dt$$

This is the easiest to use. The cosine and sine Fourier series below are a lot more difficult than just working with exponentials. The coefficients are discrete with respect to $k$ and aperiodic.

For a real-valued, even, periodic CT signal with fundamental period $T_0$, we use the cosine Fourier series:

$$x(t)=\frac{a_0}{2}+\sum _{k=1}^{\infty }{a}_k\cos (k{\omega }_{0}t);{\omega }_0=\frac{2\pi }{T_0}$$ $$a_k=\frac{2}{T_0}{\int }_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)\cos (k{\omega }_{0}t)dt;k\in {\mathbb{Z}}_{\ge 0}$$

For a real, odd, periodic CT signal, we use the sine Fourier series:

$$x(t)=\sum _{k=1}^{\infty }{b}_k\sin (k{\omega }_{0}t)$$ $$b_k=\frac{2}{T_0}{\int }_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)\sin (k{\omega }_{0}t)dt$$

Computations

We first need to periodise the signal, i.e., find some $x_{\text{fin}}(t)$ within the period. Because we can integrate over any one period, this means we should pick the easiest one. It’s sometimes easy if the interval is centred at 0.

Often the easiest period is $t\in [-\frac{T_0}{2},\frac{T_0}{2}]$ or $t\in [0,T_0]$. Both will give us the same result.

Then we first compute ${\alpha }_0$. Then we compute ${\alpha }_k$ for $k\ge 1$. Writing the closed-form summation gives us the CTFS.

Conversions

We have:

• $x(t)$ is real and even, the CTFS coefficients are real and even
• $x(t)$ is real and odd, the CTFS coefficients are complex and odd
• $x(t)$ is complex and even, the CTFS coefficients are complex and even
• $x(t)$ is complex and odd, the CTFS coefficients are real and odd

If $x$ is a real-valued $T_0$-periodic signal, the coefficients:

$${\alpha }_{-k}={\alpha }_k^{\ast }$$ $$|{\alpha }_{-k}|=|{\alpha }_k|$$

i.e., the magnitude of the coefficients is an even function of $k$.

Properties

There are many useful properties of the CTFS that we can use as “shortcuts” to find the CTFS coefficients. Much like the Laplace transform!

Orthogonality is a useful property that states for any $m,l\in \mathbb{Z}$:

$$\frac{1}{T_0}{\int }_0^{T_0}{e}^{jm{\omega }_{0}t}{e}^{-jl{\omega }_{0}t}dt=\{\begin{array}{ll}1& m=l\\ 0& m\ne l\end{array}$$

What this means is that if we compute out the sum/product of $\cos$ or $\sin$ functions, this lets us find the harmonics very easily, i.e., harmonics where the above is 1 are only valid, which allows us to find the coefficients.

Its relationship with the CTFT is as follows:¹

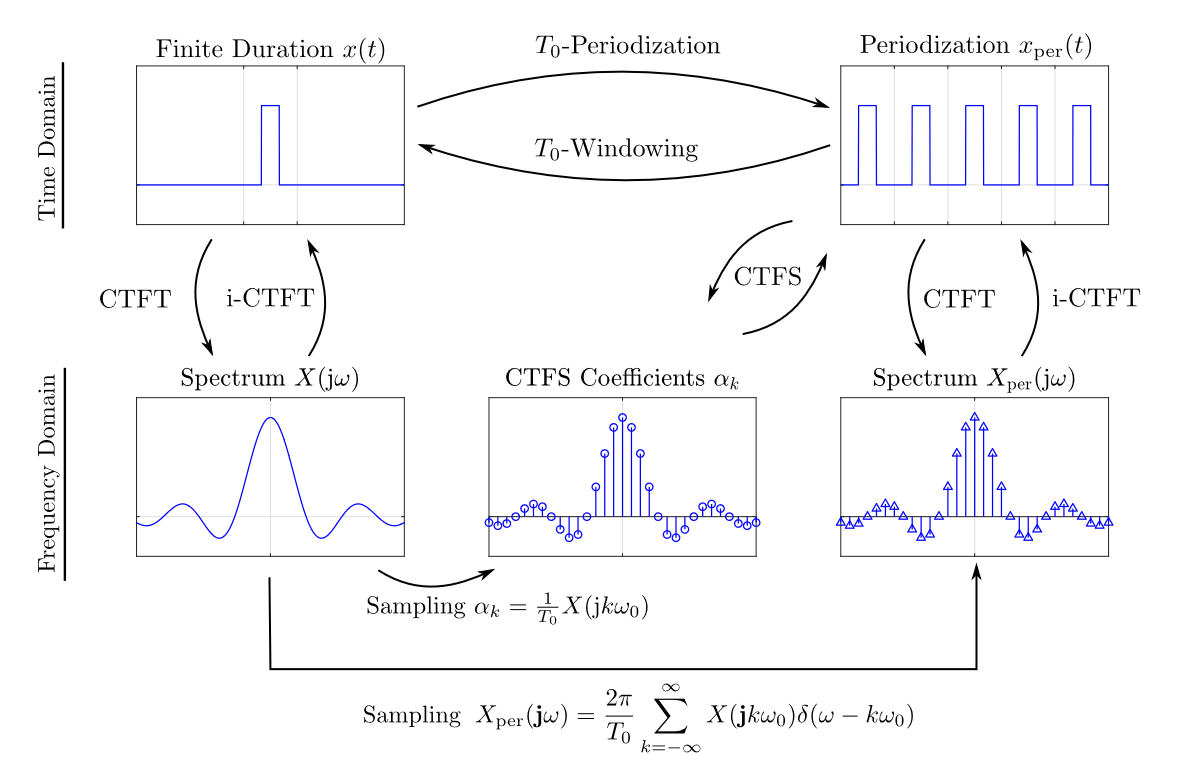
Table of properties

For functions and their coefficients: #todo For a time shift by $t_0$, $x(t-t_0)$:

$$e^{-jk{\omega }_0{t}_0}{\alpha }_k$$

A frequency shift by $k_0$, $e^{j{k}_0{\omega }_{0}t}x(t)$:

$${\alpha }_{k-k_0}$$

A complex conjugation, $x^{\ast }(t)$:

$${\alpha }_{-k}^{\ast }$$

A time-reversal, $x(-t)$:

$${\alpha }_{-k}$$

Differentiation:

$$(j{\omega }_{0}k){\alpha }_k$$

Convolution, $1/T_0{\int }_0^{T_0}x(\tau )y(t-\tau )d\tau$:

$${\alpha }_k{\beta }_k$$

Multiplication, $x(t)y(t)$:

$$\sum _{l=-\infty }^{\infty }{\alpha }_l{\beta }_{k-l}$$

The real and imaginary parts (note that they’re just the $\cos$ and $\sin$ parts respectively due to Euler’s formula):

$$\frac{1}{2}({\alpha }_k+{\alpha }_{-k}^{\ast })$$ $$\frac{1}{2j}({\alpha }_k-{\alpha }_{-k}^{\ast })$$

Premise

If we choose to restrict the number of terms of the sum, we find a pretty competent approximation and representation of the signal. The premise is that for some building block signals (sinusoids and exponentials), we can construct a new signal $\hat{x}$ with a linear combination:

$$\hat{x}={\alpha }_0{\varphi }_0+{\alpha }_1{\varphi }_1+{\alpha }_2{\varphi }_2+\cdots =\sum _k{\alpha }_k{\varphi }_k$$

where ${\alpha }_k\in \mathbb{C}$ are constant weighting coefficients. Then, if we can find $\{{\alpha }_0,{\alpha }_1,\dots \}$ such that $\hat{x}=x$, then we say $\hat{x}=x={\Sigma }_k{\alpha }_k{\varphi }_k$ is a representation of $x$ in the basis $\{{\varphi }_0,{\varphi }_1,\dots \}$.

There’s two ways we can derive the CTFS. One is to find an approximation that minimises the mean squared error (energy of the error):

$$J({\alpha }_{-K},\cdots ,{\alpha }_K)=\frac{1}{T_0}{\int }_0^{T_0}|x(t)-{\hat{x}}_K(t){|}^{2}dt$$

where we want to find constants ${\alpha }_k$ that minimises $J$. By theorem, the selection of coefficients that minimises the MSE are the CTFS coefficients. So the best possible approximation to $x$ within $2K+1$ signals is the complex exponential CTFS.

Some comments on the CTFS:

• The magnitude $|{\alpha }_k|$ tells us how strongly the frequency harmonic $k{\omega }_0$ appears in the overall signal $x$.
• The $k=0$ term in ${\hat{x}}_K(t)$ is constant; called the “DC” term”.

Prof Najm says that the Fourier series essentially breaks down signals into the superposition of sinusoids. Like how white light can diffuse into a combination of many other colours.

Related topics

• Fourier series convergence

Footnotes

1. From Prof Simpson-Porco’s lecture notes. ↩