Discrete-time Fourier series

The discrete-time Fourier series (DTFS) describes a periodic discrete-time signal in terms of a finite sum of complex DT exponential signals. This is similar to the continuous-time Fourier series.

The DTFS is given by:

$$x[n]=\sum _{k=0}^{N_0-1}{\alpha }_k{e}^{jk{\omega }_{0}n}$$

And the coefficients are given by:

$${\alpha }_k=\frac{1}{N_0}\sum _{l=0}^{N_0-1}x[l]e^{-jk{\omega }_{0}l}$$

${\alpha }_k$ captures the amount of harmonic $k{\omega }_0$ contained in $x$. Importantly, the DTFS Fourier coefficients are always periodic with period $N_0$, i.e.:

$${\alpha }_{k+N_0}={\alpha }_k\forall k$$

Both sums are finite, and both sums can be taken over any window of length $N_0$.

Computations

Make sure to leverage the orthogonality property below. If needed, convert $\sin$ and $\cos$ functions into their exponential representations.

We are not restricted by the ranges of the summation in the coefficients! We can theoretically take over any period, as we do in the CTFS.

Properties

The orthogonality property is a useful relationship:

$$\frac{1}{N_0}\sum _{n=0}^{N_0}{e}^{jm{\omega }_{0}n}{e}^{-jl{\omega }_{0}n}=\{\begin{array}{ll}1& m=l+k{N}_0;k\in \mathbb{Z}\\ 0& m\ne l\end{array}$$

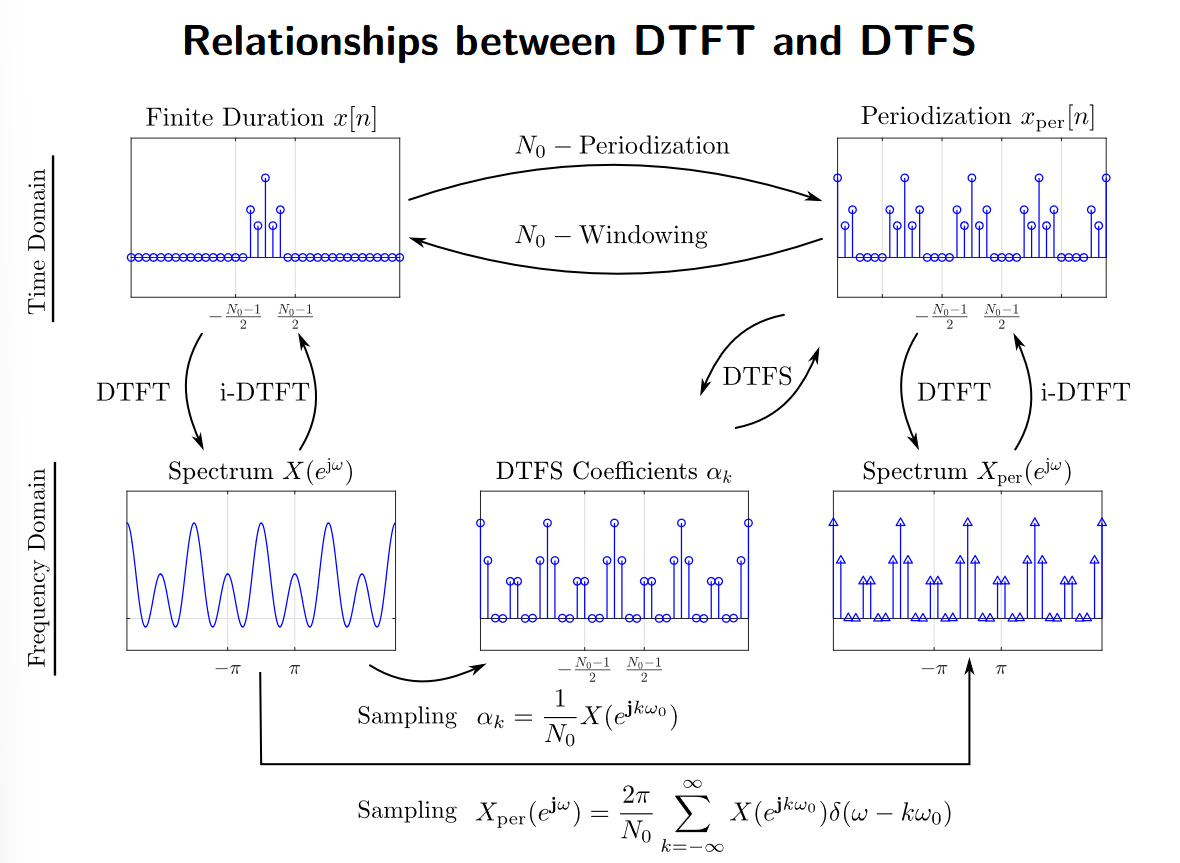
Its relationship with the DTFT is given below:¹

Footnotes

1. From Prof Simpson-Porco’s lecture notes. ↩