Signal theory

A signal is a function of one or more independent variables that contains information about a physical phenomenon. Processing these signals and interpreting them is a core question of electronic design and systems theory, which allows us to do more useful and interesting things.

Basic foundations

$n$-dimensional signals are functions of $n$ independent variables. Key examples of multidimensional signals are images (brightness as a function of $x,y$ positions, i.e., a two-dimensional signal) or video. There are two broad classes of signals: continuous-time (CT) and discrete-time (DT). The practice of engineering systems that involve both analogue and digital signal processing is called mixed-signal design.

Below is a continuous-time analogue signal and a discrete-time signal:¹

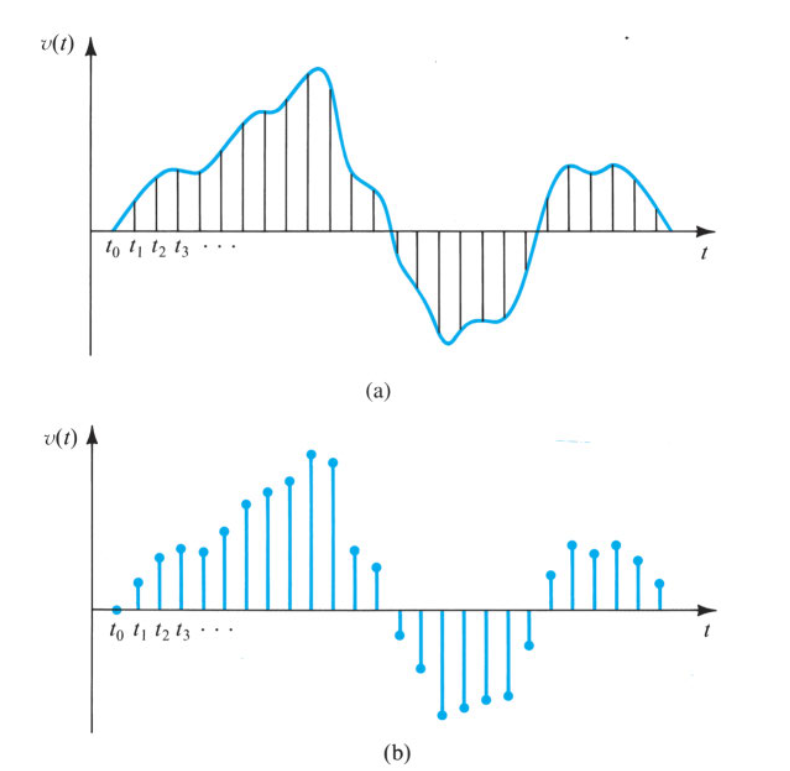
For analysis and representation, signals are commonly represented in either the time domain or the frequency domain (via the Fourier transform (continuous, discrete), Laplace transform, and the Z-transform).

Properties

Some key properties of CT/DT signals:

• Periodicity
• Even and odd
• Signal duration
• Vector spaces of signals

We additionally define the action $\Vert x{\Vert }_1$ as:²

$$\Vert x{\Vert }_1={\int }_{-\infty }^{+\infty }|x(t){|}^{1}dt$$ $$\Vert x{\Vert }_1=\sum _{-\infty }^{+\infty }|x[n]{|}^1$$

If the action is finite, then we say $x\in {\mathsf{L}}_1$ (CT) or $x\in l_1$ (DT).

The energy $\Vert x{\Vert }_2^2$ is defined as:

$$\Vert x{\Vert }_2^2={\int }_{-\infty }^{\infty }|x(t){|}^{2}dt$$ $$\Vert x{\Vert }_2^2=\sum _{n=-\infty }^{\infty }|x[n]{|}^2$$

If the energy is finite, then we say $x\in {\mathsf{L}}_2$ (CT) or $x\in l_2$ (DT). The intuition comes from standard definitions for power.

The amplitude $\Vert x{\Vert }_{\infty }$ is defined as:

$$\Vert x{\Vert }_{\infty }=\underset{t\in \mathbb{R}}{\max }|x(t)|$$ $$\Vert x{\Vert }_{\infty }=\underset{n\in \mathbb{Z}}{\max }|x[n]|$$

If the amplitude is finite, we say $x\in {\mathsf{L}}_{\infty }$ (CT) or $x\in l_{\infty }$ (DT). Finite amplitude signals are bounded signals, i.e., $|x(t)|$ is bounded by a constant.

For periodic signals, we simply restrict the integrals and sums to one period $[0,T_0]$, and distinguish the vector spaces with ${\mathsf{L}}_i^{\text{per}}$ or $l_i^{\text{per}}$.

Operations

CT/DT signals share several key basic operations:

• Pointwise operations, i.e., operates on the whole signal for $t\in \mathbb{R}$
  • Addition: $h(t)=f(t)+g(t)$
  • Scaling, by a constant $\alpha$: $h(t)=\alpha f(t)$
  • Multiplication: $h=f\cdot g$, $h(t)=f(t)g(t)$
• Time-shift, by $t_0\in \mathbb{R}$ or $n_0\in \mathbb{Z}$ for $x(t-t_0)$ and $x[n-n_0]$; shifting horizontally
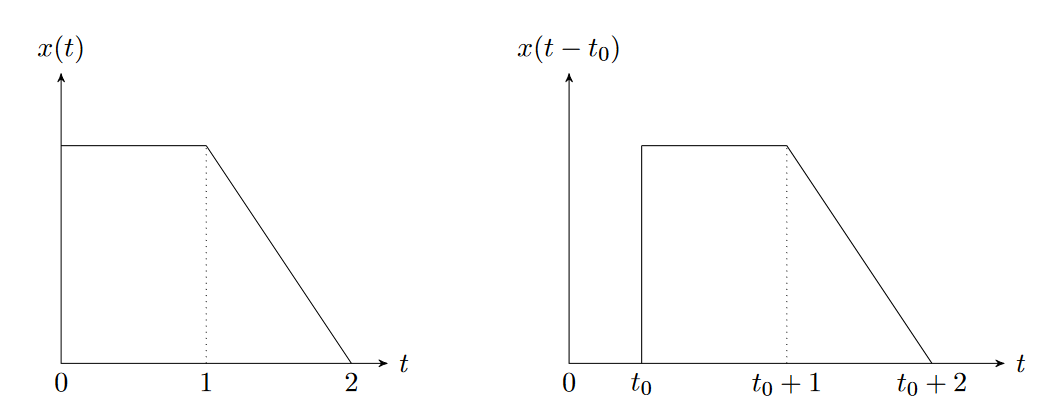
  • This is exactly how it looks: a positive $t_0,n_0$ means the signal is shifted to the right and we delay in time. Otherwise we advance in time.
• Time-scaling can compress or expand the signal by time:
  • For a CT signal, $x(\alpha t)$, we compress for $|\alpha |>1$, expand for $|\alpha |<1$. If $\alpha <0$, the time effectively flips (i.e., it’s reflected about some axis of symmetry).
  • For a DT signal, $x[\alpha n];\alpha \in \mathbb{Z}$, we’re effectively sub-sampling the signal. For example, if we have $\alpha =2$, then we keep only every other sample.

Signal operations can be compounded to obtain more complicated signals. We want to start with time scaling then time shifting when composing signals.

Sub-pages

• Types of signals
  • Unit step function
  • Impulse function
  • Sinusoid
  • Exponential function
• Continuous-time signal
  • Continuous-time Fourier series
  • Continuous-time Fourier transform
  • Laplace transform
• Discrete-time signal
  • Discrete-time Fourier series
  • Discrete-time Fourier transform
  • Discrete-time system
• Signal processing
  • Digital signal processing

Resources

• ECE216 — Signals and Systems
  • Signals and Systems, by W. Murray Wonham (1996)
  • Signals and Systems, by Stark C. Draper (2020)
  • Signals and Systems, by John Simpson-Porco (2024)
• Signals and Systems, by Alan Oppenheim
• Video lectures
  • RES.6.007 — Signals and Systems (MIT, Alan Oppenheim, 1987)
  • MATH 334 — The Mathematical Theory of Signals and Systems (Queen’s, Andrew D. Lewis, 2022); also five volume reference textbook

Footnotes

1. From Microelectronic Circuits, by Sedra/Smith. ↩

2. Note that because we deal with a discrete signal, we don’t need the continuous sum (i.e., an integral). ↩