Signal duration

In signal theory, we define the duration of a signal $x$ as finite if it equals zero outside some bounded time interval. Otherwise, it is of infinite duration. The notion of finite-duration signals allows us to construct the notion of periodic signals as the infinite sum of time-shifted finite-duration signals.

The support $\text{supp}(x)$ of a signal essentially tells us where the signal is non-zero:

• CT case: the smallest set containing $\{t\in \mathbb{R}\mid x(t)\ne 0\}$.
• DT case: the set $\{n\in \mathbb{Z}\mid x[n]\ne 0\}$.

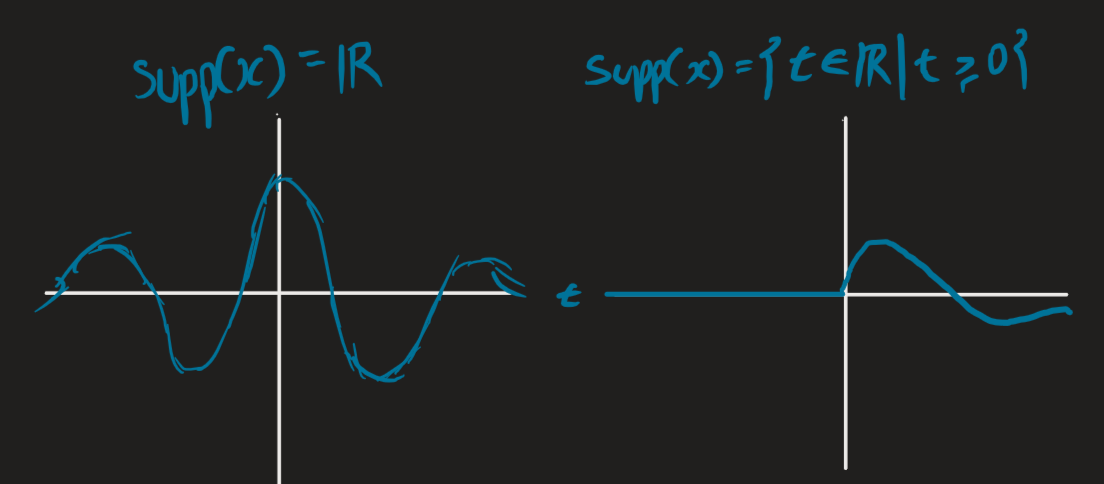i.e., it is a finite duration signal if $\text{supp}(x)$ is contained in a bounded interval.

Signals often “begin” at some time. We say that a signal (CT/DT) is:

• Right-sided from time $T$ or $N$ if $x(t)=0\forall t<T$.
• Right-sided if it’s right-sided from time $T$ for some $T$.