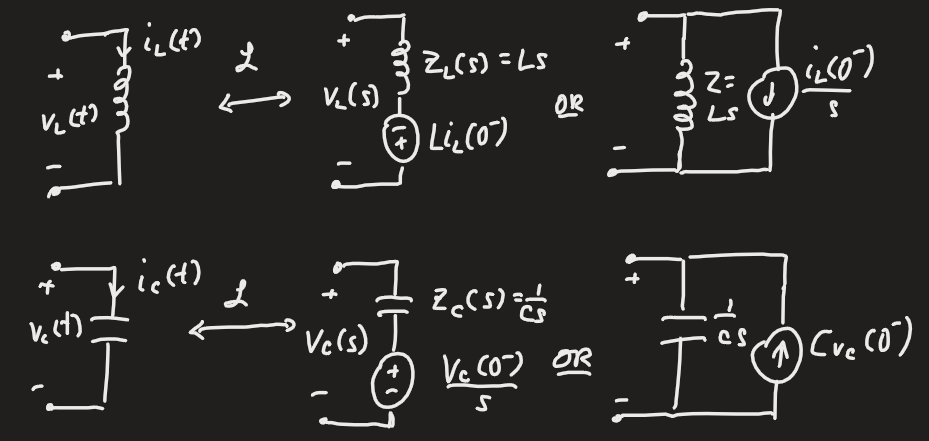Frequency domain

In signals and systems analysis, the frequency domain (also s-domain, Laplace domain) describes the range of frequencies at which a given system (circuit or otherwise) operates.

We can transform time domain connection and element constraints to algebraic equations in the $s$-domain. Kirchhoff’s laws still hold. Transformations can be done with the Laplace transform or the Fourier series/Fourier transform. The Fourier transform is especially useful because it can represent signals as sums of sinusoids with varying frequencies and amplitudes.

Links with the phasor domain

At a high level, phasor domain looks at sinusoidal behaviour at a certain frequency. On the Laplace side, if our circuit has a sinusoidal input, then we can generalise the behaviour for all frequencies. Then, at a given frequency $\omega$, our circuit is functionally back in the phasor domain.

Circuit analysis

For a resistor:

$$V(s)=RI(s)$$

For an inductor:

$$V(s)=LsI(s)-Li(0^{-})$$ $$I(s)=\frac{1}{Ls}V(s)+\frac{i(0^{-})}{s}$$

For a capacitor:

$$I(s)=CsV(s)-Cv(0^{-})$$ $$V(s)=\frac{1}{Cs}I(s)+\frac{v(0^{-})}{s}$$

In particular, if a circuit has non-zero initial conditions, we can replace time domain circuits with equivalent s-domain circuits: