Impulse response

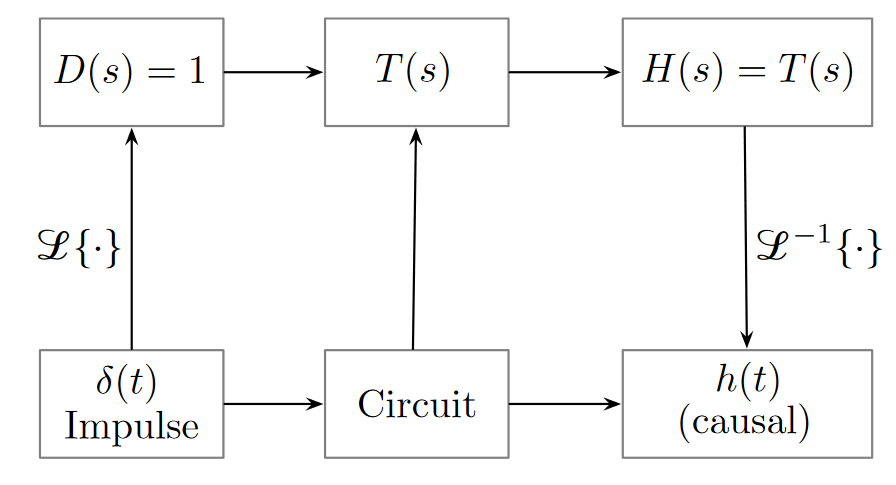
The impulse response is the output signal $h(t)$ of an linear time-invariant system where the input signal is the impulse function $\delta (t)$. We can write:

$$H(s)=T(s)\Delta (s)=T(s)\mathcal{L}\{\delta (t)\}=T(s)$$

What this means is the impulse response exactly captures the system’s transfer function, whether in the Laplace domain or the time domain. This implication is useful because we can reveal what happens in the system by driving it with an impulse input.

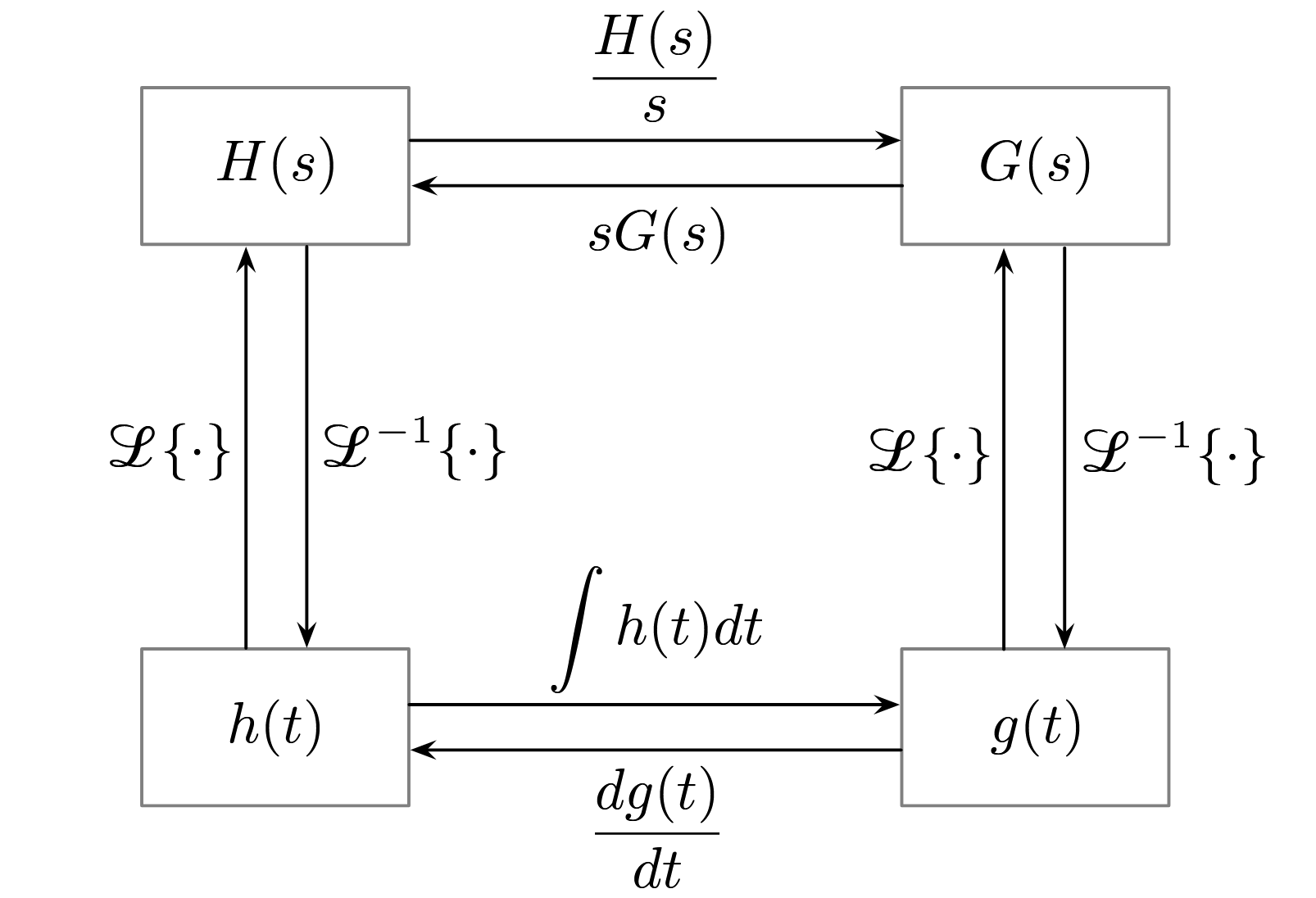
The relationship between everything looks like: We can also calculate the impulse response by applying the unit step function and differentiating the output:

Properties

If all the poles of the transfer function have negative real parts, then the impulse response decays to zero over time and the circuit is stable.

By theorem, an LTI system with impulse response $h$ is:

• Causal if and only if $h(t)=0\forall t<0$.
• Memorylessness if and only if $h(t)=\alpha \delta (t)$, for some $\alpha \in \mathbb{C}$.
• BIBO stable if $h\in {\mathsf{L}}_1$. If it is, then: $\Vert y{\Vert }_{\infty }\le \Vert h{\Vert }_1\Vert x{\Vert }_{\infty }\forall x\in {\mathsf{L}}_{\infty }$.

With some notational changes this also applies for DT systems. Note also that $T$ is invertible if and only if there exists another impulse response $h_{\text{inv}}$ such that $h\ast h_{\text{inv}}=\delta$. So the inverse of an LTI system is also an LTI system.

Computations

Laplace domain

In general, we can find the impulse response:

$$h(t)=y(t)={\mathcal{L}}^{-1}\{H(s)X(s)\}$$

We may have to do some partial fraction decomposition to get something we can easily take the inverse Laplace transform of. This is pretty straightforward usually.

Time domain

Any time domain output response is given by the convolution:

$$y(t)={\int }_0^{t}h(t-\tau )x(\tau )d\tau =h\ast x$$

where $h$ is the transfer function and $x$ is any input signal. Note that since the variable of integration is $\tau$, any $t$ term is functionally constant here.

Take note of any cases where the unit step function is in the integral. If there’s no offset, i.e., $u(t)$, then we can ignore it since the convolution’s lower bound is at $t=0$. We can change the bounds if the step function is offset.

See also

• Finite impulse response