Causality

Causality is a systems property. A CT system $T$ is causal if $\forall t\in \mathbb{R}$, the output $y$ depends only on the past and present input values, $x(\tau {)}_{\tau \le t}$. What this means intuitively is that the system doesn’t “look into the future”. Note that all models of physical systems are causal (which intuitively makes sense!). A special case of causality is a system that is memoryless.

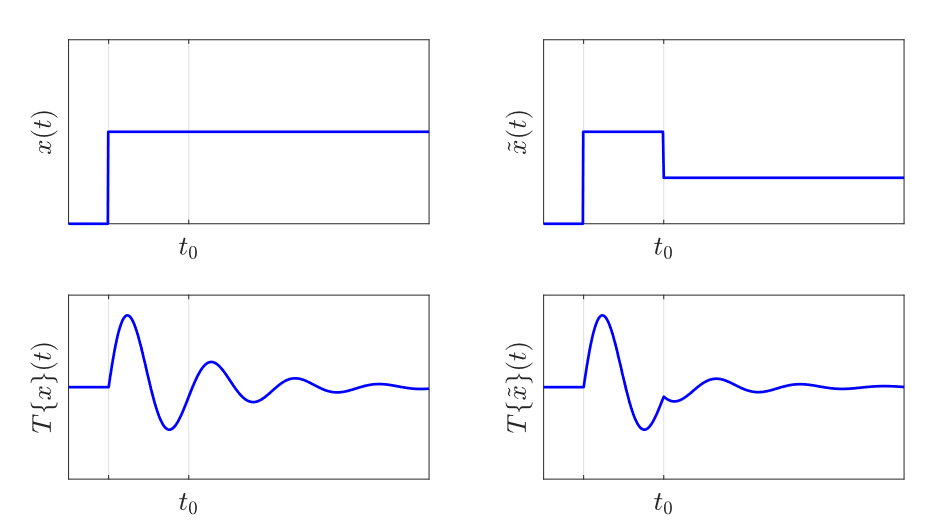
An equivalent definition states that a system is causal if for any time $t_0$, and two inputs $x,\tilde{x}$ that satisfy $x(t)=\tilde{x}(t)\forall t\le t_0$, then the corresponding outputs satisfy $y=\tilde{y}\forall t\le t_0$. Geometrically, this means that if the inputs line up until some time $t$, then the corresponding outputs must also line up until that time.

A linear CT system $T$ is causal only if for any time $t_0$ and any input $x$ such that $x(t)=0\forall t\le t_0$, the output $y=T\{x\}$ satisfies $y(t)=0\forall t\le t_0$. If a right-sided input from time $t_0$ produces a right-sided output from time $t_0$, then the system is causal.

Theorem

By theorem, for a causal LTI system with impulse response $h=T\{\delta \}$, if $x$ is right-sided from time 0, then $y$ is right-sided from time 0 and:

$$y(t)={\int }_{-\infty }^{\infty }h(t-\tau )x(\tau )d\tau ={\int }_{0^{-}}^{t}h(t-\tau )x(\tau )d\tau ,t\le 0$$

See the below.¹ Note how $x$ and $\tilde{x}$ line up until $t_0$. Their outputs also line up until that time! Causal systems can be checked by inspection. Does the explicit formulation of the system depend on values of $t\ge \tau$? If so, we know the system is not causal.

Footnotes

1. From Prof Simpson Porco’s lecture notes. ↩