Transfer function

In system theory, a system where inputs and outputs are in different (i.e., two) ports, the system’s network function is called a transfer function. These functions are in the Laplace domain, and find wide use in figuring out what exactly the function does. 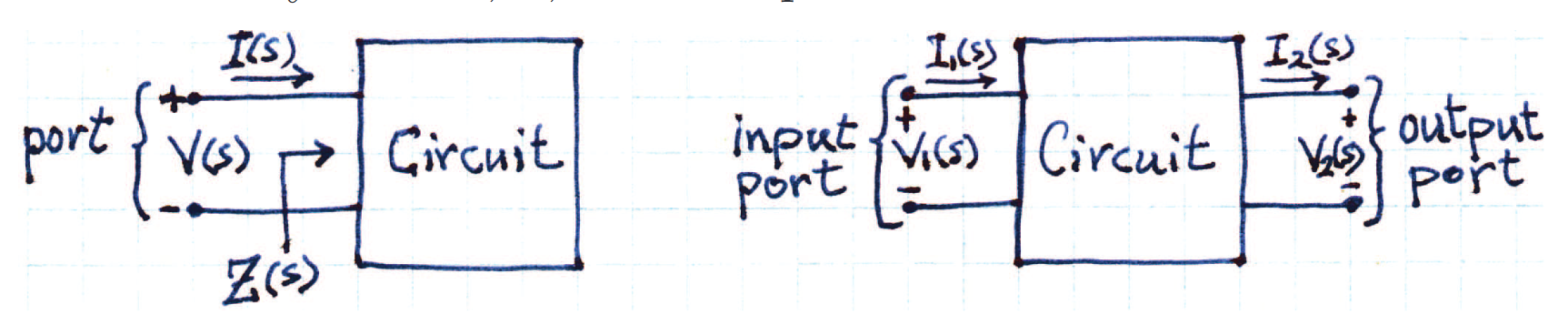There are four main types of transfer functions:

• $T_V(s)=V_2(s)/V_1(s)$, voltage transfer function, unitless
• $T_I(s)=I_2(s)/I_1(s)$, current transfer function, unitless
• $T_Y(s)=I_2(s)/V_1(s)$, transfer admittance, siemens
• $T_Z(s)=V_2(s)/I_1(s)$, transfer impedance, ohms

We refer to the magnitude of the transfer function as the gain function and the angle as the phase function. Both are frequency dependent, which can sometimes be bad news. Signals are usually the sum of many contributions at many frequencies. Different gains to different components results in noise — i.e., we distort the signal and its lost fidelity.

Note that while we normally have an open circuit, when we measure the output current we take a short circuit between the terminals. Importantly, the transfer function can be determined by the impulse response, where we input the impulse function. 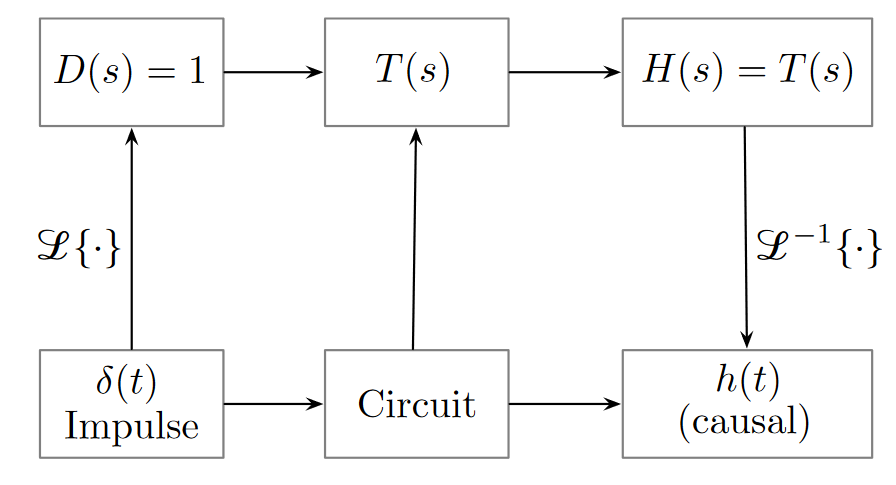When $T(s){|}_{s=j\omega }$, we have a gain function. The angle of this function is called the phase function. More on that at the page on frequency response.

More complicated systems

We usually refer to $T(s)$ as the forward transfer function (left to right) and $T^{\prime }(s)$ as the reverse transfer function (opposite). In general, they’re not reversible: $T(s)\ne 1/T^{\prime }(s)$, i.e., if we apply a signal at the output port, we won’t get the inverse transformation.

When we connect two circuits in a cascading format as followed: 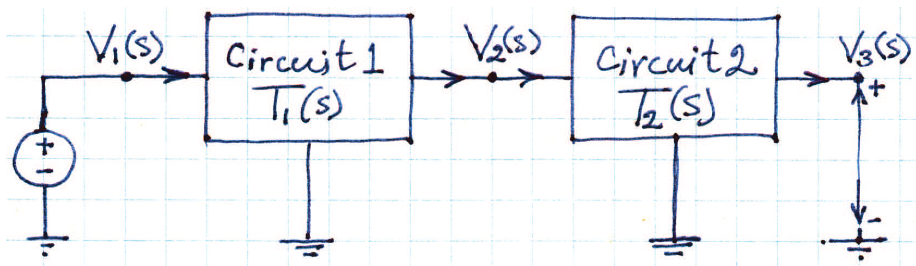the transfer function of the full circuit is:

$$T(s)=T_1(s)T_2(s)=\frac{K_{1}s}{s+{\alpha }_1}\times \frac{K_2}{s+{\alpha }_2}$$

When we have two circuits connected in parallel: 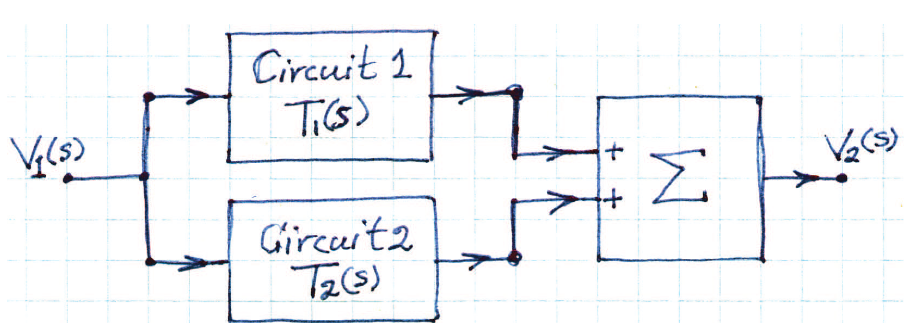the transfer function is:

$$T(s)=T_1(s)+T_2(s)$$

Domain conversions

From a state-space model

Say we have a state-space model:

$$\dot{x}=Ax+Bu$$ $$y=Cx+Du$$

We then take the Laplace transform of both equations, such that we get:

$$sX(s)=AX(s)+BU(s)$$ $$Y(s)=CX(s)+DU(s)$$

Then, we can rewrite such that:

$$X(s)=(sI-A{)}^{-1}BU(s)$$ $$Y(s)=(C(sI-A{)}^{-1}B+D)U(s)$$

where $I$ is the identity matrix, and $s$ is a regular Laplace frequency unit. The $Y(s)$ term in the brackets is the transfer function $G(s)$.

$$G(s)=\frac{Y(s)}{U(s)}=C(sI-A{)}^{-1}B+D$$

We can hand compute the inverse matrix using the determinant and adjoint matrix.

$$(sI-A{)}^{-1}=\frac{1}{\det (sI-A)}\text{adj}(sI-A)$$