State-space model

A state-space model consists of $n$ coupled first-order non-linear differential equations, with $n$ state variables, $m$ excitation input variables, and $k$ output variables. These find use in small signal analysis and control systems. This analysis converts an $n$th order DE into $n$ first-order DEs, by essentially recursively defining each ODE.

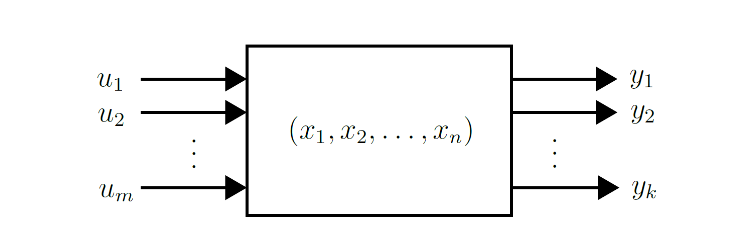
Definition

We call the differential equations state space equations.

$$\frac{d{x}_1}{dt}=f_1(x_1(t)\dots x_n(t),u_1(t)\dots u_m(t))$$ $$\frac{d{x}_n}{dt}=f_n(x_1(t)\dots x_n(t),u_1(t)\dots u_m(t))$$

Observe that the first-order time derivatives of the state variables are on the left side. The functions on the right have inputs of the state variables and the excitation inputs. We also define $k$ output equations that depend on the $n$ state variables and $m$ input signals:

$$y_1=g_1(x_1(t)\dots x_n(t),u_1(t)\dots u_m(t))$$ $$y_k=g_k(x_1(t)\dots x_n(t),u_1(t)\dots u_m(t))$$

And we define system equations as an equation set comprised of state space equations (that describe the dynamics of the system) and output equations.

We can rewrite this model in terms of matrix representations, only if the system is linear:

$$x=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_n\end{array}\right],B=\left[\begin{array}{c}{b}_1\\ ⋮\\ b_n\end{array}\right]$$ $$A=\left[\begin{array}{c}{a}_{11}\cdots a_{1n}\\ ⋮\ddots ⋮\\ a_{n1}\cdots a_{nn}\end{array}\right]$$ $$D=d,C=[c_1,c_2,\cdots ,c_n]$$

Then:

$$\dot{x}=Ax+Bu$$ $$y=Cx+Du$$

We define:

• $\vec{x}$ — state vector.
• $u$ — input signal, scalar function.
• $\vec{y}$ — output signal vector.
• $A$ — state matrix for the system, $A\in {\mathbb{R}}^{n\times n}$. Consists of scalar values.
• $B$ — input matrix, $B\in {\mathbb{R}}^{n\times m}$.
• $C$ — output matrix.
• $D$ — feed-forward matrix. Note that in most examples, this mechanism doesn’t exist (so $D=0$).

Creating equations and matrices

We use a recursive definition of our state variables. For example, if we define:

$$x_1(t)=y(t)$$

Then, we define:

$$x_2(t)=\frac{dy(t)}{dt}={\dot{x}}_1(t)$$

And so on, such that for each successive definition of $x_i$, we depend on the definition of $x_{i-1}$. This is how we create our first-order differential equations.

Conversions

To time-domain

To get a time domain response, we must maintain the IVP. Then:

$$\Phi (s)=(sI-A{)}^{-1}$$ $$X(s)=\Phi (s)x(0)+\Phi (s)BU(s)$$ $$x(t)=\Phi (t)x(0)+{\int }_0^t\Phi (t-\tau )Bu(\tau )d\tau$$

${\mathcal{L}}^{-1}\{\Phi (s)\}$ largely comes from the intuition behind ${\mathcal{L}}^{-1}\{(s-\alpha {)}^{-1}\}$. Since we have a multiplication in the frequency domain, we get a convolution in the time domain.

From transfer function

Say we have a transfer function $T(s)=\frac{Y(s)}{U(s)}$. Say also that the time domain conversion doesn’t facilitate creating a state-space model (for example, if $u(t)$ had multiple derivative terms). We can convert to a state-space model still:

$$T(s)=\frac{Y(s)}{U(s)}\cdot \frac{Z(s)}{Z(s)}$$

Then, to find the input equation for $\dot{x}$, we take the inverse Laplace transform of:

$${\mathcal{L}}^{-1}\{U(s)Z(s)\}=\dot{x}$$

And, for $y$, we do the same thing:

$${\mathcal{L}}^{-1}\{Y(s)Z(s)\}=y$$