Determinant

If $A$ is some square matrix, the determinant of $A$ is some scalar associated with $A$.

In MATLAB, we can use det(A), and in NumPy with np.linalg.det(A).

Expansion

We have a few different ways of evaluating determinants by hand. Probably the most important is Laplace expansion (or cofactor expansion). We can either expand down the columns:

$$\text{det}(A)=\sum _{i=1}^n(-1{)}^{i+j}{a}_{ij}\text{det}(A_{ij})$$

or along the rows:

$$\text{det}(A)=\sum _{j=1}^n(-1{)}^{i+j}{a}_{ij}\text{det}(A_{ij})$$

The gist of this is simple: to compute the determinant of $A$, we usually examine the values of the first row and make our way right or the first column and make our way down. We take that value, multiply it by $(-1{)}^{n+1}$, then draw two lines to exclude that value’s row and column.

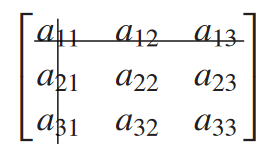
We then take the determinant of the sub-matrix contained by these lines, and continue value by value.

Properties

If $A$ and $B$ are square matrices, and $n\in \mathbb{R}$:

$$\text{det}(A)=\text{det}(A^T)$$ $$\text{det}(AB)=\text{det}(A)\cdot \text{det}(B)$$ $$\text{det}(A^n)=(\text{det}(A){)}^n$$

If $A$ is invertible:

$$\text{det}(A^{-1})=\frac{1}{\text{det}(A)}$$

Some additional properties:

• A square matrix is invertible if and only if $\text{det}(A)\ne 0$.
• For an upper or lower triangular matrix, the determinant is the product of the diagonal entries of the matrix.
• If $A$ and $B$ are similar, then $\text{det}(A)=\text{det}(B)$.
• The determinant of an orthogonal matrix is either $1$ or $-1$.

We can also relate elementary row operations with determinants. Say $B$ is obtained from manipulating $A$ in some way.

• If we divide a row of $A$ by a scalar $k$, then $\text{det}(B)=\frac{1}{k}\text{det}(A)$.
• If we swap a row, then $\text{det}(B)=-\text{det}(A)$.
• If we add a multiple of $A$ to another row, then $\text{det}(B)=\text{det}(A)$.

$2\times 2$ and $3\times 3$ matrices

We end up having some nice properties of determinants of $2\times 2$ matrices. For some matrix $A=\left[\begin{array}{ccc}a& & b\\ c& & d\end{array}\right]$, the determinant is the scalar $ad-bc$.

Determinant and invertibility theorem

If $A$ is a $2\times 2$ matrix and invertible, then:

$$A^{-1}=\frac{1}{\text{det}(A)}\left[\begin{array}{ccc}d& & -b\\ -c& & a\end{array}\right]$$

For $3\times 3$ matrices, if $A=[\vec{u}\vec{v}\vec{w}]$, then:

$$\text{det}(A)=\vec{u}\cdot (\vec{v}\times \vec{w})$$

Recall from the cross product, that the magnitude $\Vert \vec{v}\times \vec{w}\Vert$ is the area of a parallelogram spanned by the two vectors. We extend to ${\mathbb{R}}^3$, where the above is the formula for the volume of a parallelepiped.