Asymptotic tracking

Two of our main goals when designing system controllers relate to asymptotic tracking of the error signal. Recall, where the error signal is $e(t)=r(t)-y(t)$:

• For all reference signals $r(t)$, when $d(t)=0$, the asymptotic tracking error $e(\infty )$ should be bounded or converge to zero.
• For all disturbance signals $d(t)$ and for all reference signals $r(t)$, the asymptotic tracking error $e(\infty )$ is bounded or is zero.

Recall that $G(s)$ is the transfer function for the system, and that $C(s)$ is the controller’s transfer function. The transfer function between $R(s)$ and $E(s)$ is $\frac{1}{1+CG}$, called the sensitivity function. When $CG$ has $k$ poles at $s=0$, then $CG$ is of type $k$.

To generalise past polynomial reference signals, we rely on the internal model principle. In general, if any zeroes of $G(s)$ are poles of $R(s)$, then the tracking problem has no solution.

Polynomial reference signals

For any $r(t)$ in the class of polynomial reference signals with order $k-1$, then the following holds (by theorem):

• If $CG$ has $k-1$ poles at $s=0$, then:

$$\underset{t\to \infty }{\lim }e(t)=e(\infty )=\{\begin{array}{ll}\frac{\tilde{c}}{1+C^{\prime }(0)G^{\prime }(0)}& \text{if }k=1\\ \frac{\tilde{c}}{C^{\prime }(0)G^{\prime }(0)}& \text{if }k>1\end{array}$$

• If $CG$ has $k$ poles at $s=0$, then:

$$\underset{t\to \infty }{\lim }e(t)=e(\infty )=0$$

• If $CG$ has less than $k-1$ poles at $s=0$, then:

$$\underset{t\to \infty }{\lim }e(t)=e(\infty )=\pm \infty$$

If $G(s)$ has no poles at $s=0$ or less than $k$ poles, we need to add poles to $C(s)$. However, we have to keep in mind two key principles. The first is that $\frac{1}{1+CG}$ must be BIBO stable with no unstable zero-pole cancellations (i.e., poles in RHP). The second is that $e(\infty )=0$.

We add poles as necessary. For example, a PI controller adds a pole at 0 and things work out fine. Note that some tracking problems are unsolvable. In general, if $G(s)$ has any zeroes at $s=0$, then it’s impossible to achieve asymptotic tracking for polynomial reference signals.

Steady-state error

As usual, we’re interested in the steady-state error. By the final-value theorem:

$$\underset{t\to \infty }{\lim }e(t)=\underset{s\to 0}{\lim }sE(s)$$

The final-value theorem only holds if $E(s)$ is asymptotically stable and $E(s)$ has no more than 1 pole at 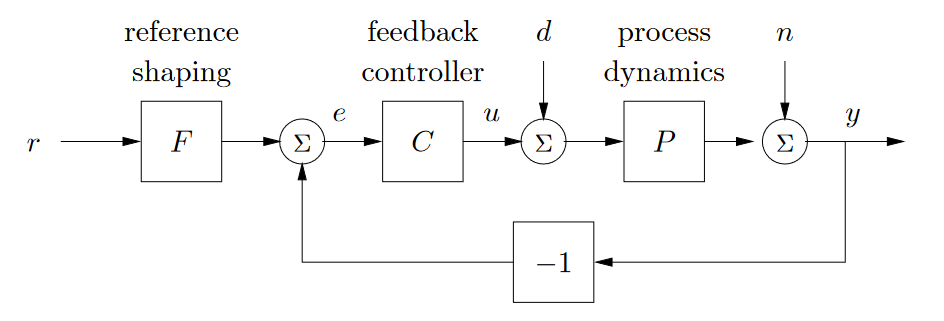$s=0$. Then, we can find $E(s)$ as follows:

$$E(s)=\frac{1}{1+C(s)P(s)}R(s)-\frac{P(s)}{1+C(s)P(s)}D(s)$$