System controller

In control theory, a controller is used within a closed-loop system to allow it to enforce a key set of performance characteristics, like stability, transient parameters, or steady-state tracking.

Tracking problem

One core problem is the tracking problem, where we want to design a controller $C(s)$ such that:

• The feedback loop system is BIBO stable.
• For all reference signals $r(t)$, when $d(t)=0$, the asymptotic tracking error $e(\infty )$ is either bounded or converges to zero, i.e., when there’s no disturbance, the system should track the reference system.
• For all disturbance signals $d(t)$ and for all reference signals $r(t)$, the asymptotic tracking error $e(\infty )$ is bounded or is zero.

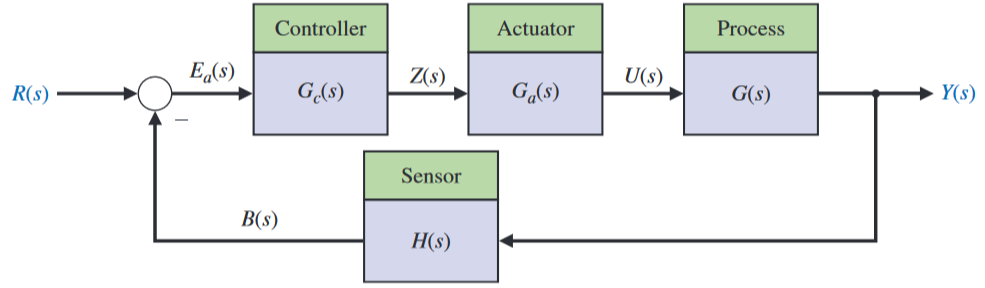The feedback system is BIBO stable if for any bounded signals $r(t),d(t)$ the signals $u(t),e(t)$ are bounded as well, where $e(t)=r(t)-y(t)$. If $r(t),e(t)$ are bounded, then $y(t)$ is also bounded.

We can model this in a system of two equations:

$$\left[\begin{array}{c}E(s)\\ U(s)\end{array}\right]=\left[\begin{array}{cc}{F}_{11}(s)& F_{12}(s)\\ F_{21}(s)& F_{22}(s)\end{array}\right]\left[\begin{array}{c}R(s)\\ D(s)\end{array}\right]$$

The system is BIBO stable if and only if all the transfer functions in the matrix above are BIBO stable.

Classes of controllers

There are a few basic important types of controllers:

Proportional controllers take the form:

$$G_C(s)=K$$

Proportional-integral (PI) controllers take the form:

$$C(s)=k\left(1+\frac{1}{Ts}\right)=k\left(\frac{Ts+1}{Ts}\right)$$

Proportional-integral-derivative (PID) controller take the form:

$$G_C(s)=K_p\left(1+\frac{1}{T_{i}s}+T_{d}s\right)$$

Lead controllers take the form:

$$C(s)=k\frac{T+1}{\alpha T+1}$$

Lag controllers take the form:

$$C(s)=\alpha \frac{T+1}{\alpha T+1}$$