Routh-Hurwitz criterion

In control theory, the Routh-Hurwitz criterion is a necessary and sufficient criterion for proving the BIBO stability of LTI systems. For a characteristic polynomial (the denominator of the transfer function) of a stable system $q(s)$, the number of roots of $q(s)$ with positive real parts must be equal to the number of changes in sign of the first column of the Routh array.

For a stable system, there must be no changes in sign in the first column.

The Routh array is given by: 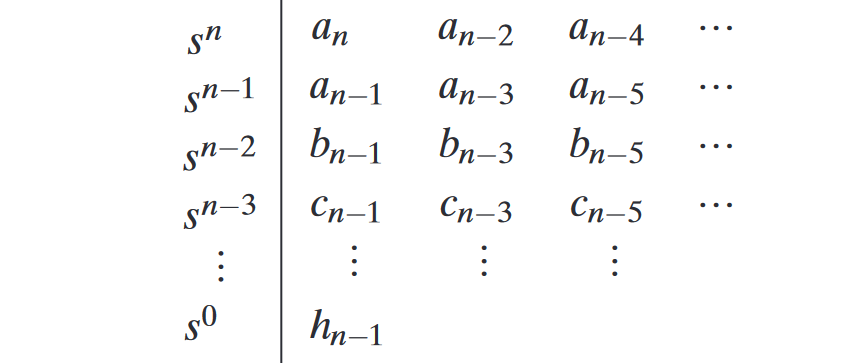Where the corresponding $b$ and $c$ terms are given by:

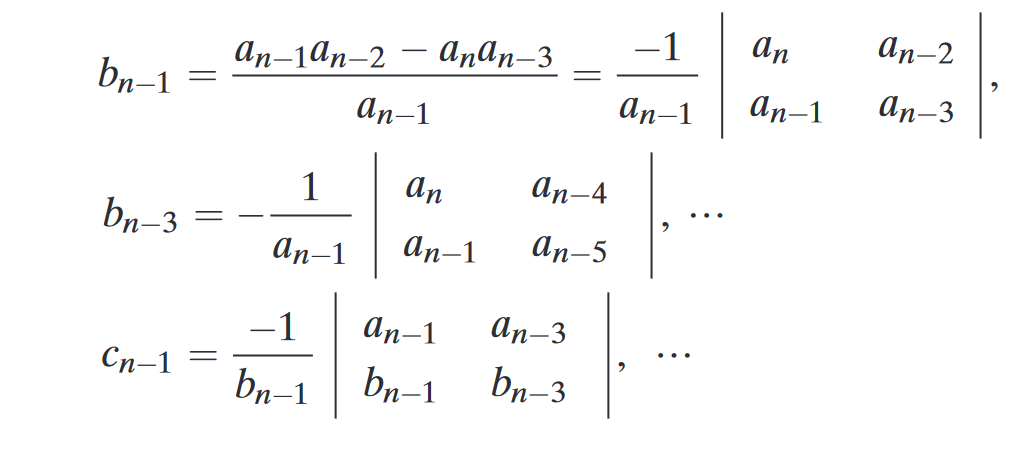
Interpretation

We have several cases for the elements in the first column:

• No element is zero — then by definition, all the coefficients must be positive or all must be negative.
• There’s a zero in the first column, but some other elements of the containing row are non-zero — we can in fact replace that 0 with an arbitrarily small positive number $ϵ$ that can approach zero.
• There’s a zero in the first column, and all other elements of the containing row are zero — in this case, we look at the row before the zero row, which contains the auxiliary polynomial $U(s)$. The auxiliary polynomial reveals the roots of $q(s)$.
• Repeated roots of the characteristic equation on the $j\omega$-axis — if we have duplicated auxiliary polynomials, we have repeated roots on the $j\omega$-axis, implying the system is unstable.