Inverse relation

A map (function, linear map, system) $T:X\to Y$ is invertible if there is a unique solution $x\in X$ for every $y\in Y$. In other words, an inverse relation $T^{-1}$ will map the inverse operation of 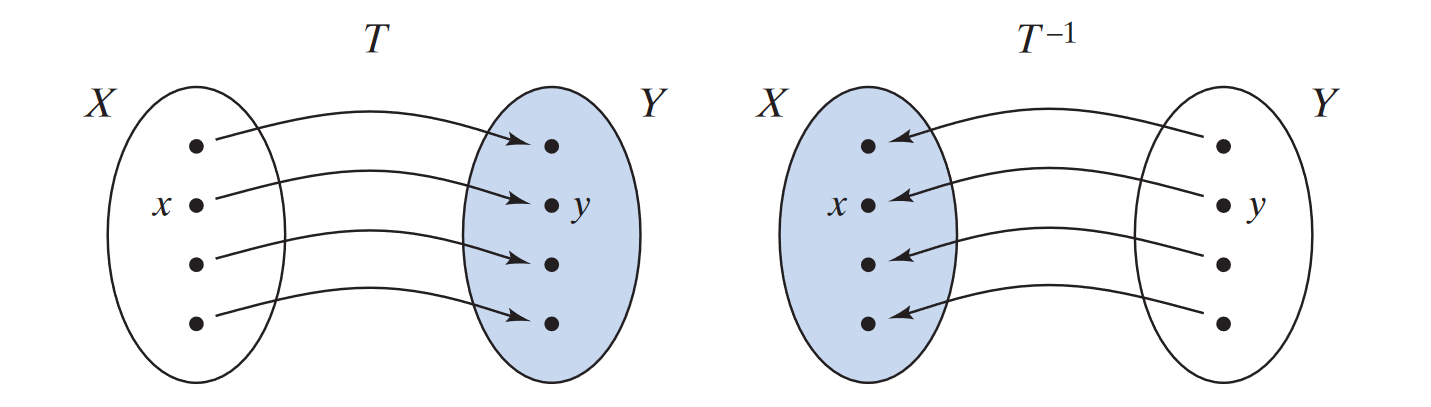$T$. $T$ must be bijective (i.e., injective and surjective) to be invertible.

Linear transformation

The property of bijectivity leads to many useful tools that we can use to find if a linear transformation is invertible.

• $\text{rref}(A)=I_n$, i.e., there is a pivot in each row and column
• $\text{rank}(A)=m=n$, i.e., it is square
• The linear system $A\vec{x}=\vec{b}$ has a unique solution $\vec{x}$ for all $\vec{b}$ in ${\mathbb{R}}^n$
• $\text{im}(A)={\mathbb{R}}^n$
• $\text{ker}(A)=\vec{0}$
• $\text{det}(A)\ne 0$

By theorem:

$$I_n=A{A}^{-1}=A^{-1}A$$

A square matrix that is non-invertible is singular. Since matrix inversion isn’t defined for matrices that aren’t square, this motivates the idea of the Moore-Penrose pseudoinverse, which allows us to use singular value decomposition to find an approximate solution that is as close to valid as possible (since we might have infinitely many solutions or none at all).

Systems

An LTI system $T$ is invertible with impulse response $h$ if and only if there exists an impulse response $h_{\text{inv}}$ for the system $T_{\text{inv}}$ such that $h\ast h_{\text{inv}}=\delta$. If we then take the {C/D}TFT of both sides, then:

$$h\ast h_{\text{inv}}=\delta ⟷H{H}_{\text{inv}}=1$$

$T$ is invertible if and only if $H(j\omega )\ne 0\forall \omega \in \mathbb{R}$.

How do we exactly find this? Using the frequency response property (that the product is 1), once we find a closed-form expression for $H(j\omega )$, we can find a suitable inverse expression for $H_{\text{inv}}$.

Additionally, a system $T$ is invertible if there exists a system $T_{\text{inv}}$ such that:

$$T_{\text{inv}}\{T\{x\}\}=T\{T_{\text{inv}}\{x\}\}=x$$

for all inputs $x$.