Injectivity

A map $f:A\to B$ (i.e., a function or linear transformation) is injective (or one-to-one) if each element in the domain maps to a unique element in the codomain. Formally this means that if $a_1\ne a_2$ in $A$, this implies that 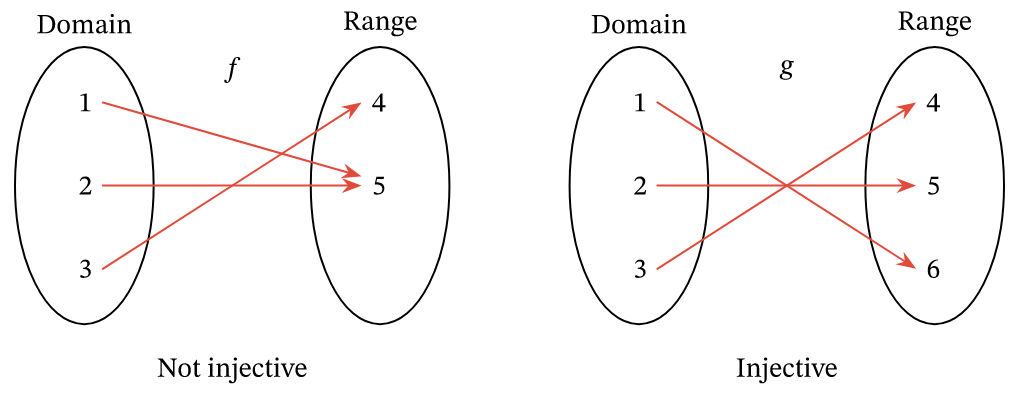$f(a_1)\ne f(a_2)$ in $B$. A linear map $T:{\mathbb{R}}^m\to {\mathbb{R}}^m$ is injective if and only if the zero vector is the only element in the kernel of $T$, i.e., $\text{ker}(T)=\vec{0}$. An easy way to tell if $T$ is injective is if there’s a pivot in each column after row reducing.

See also

• Surjectivity
• Bijectivity