Kernel subspace

The kernel of a linear transformation is a subspace that is the set of all values that the map inputs and has a result of the zero vector, $\vec{0}$. For $T:{\mathbb{R}}^m\to {\mathbb{R}}^n$, the kernel is in the set of the domain, i.e., $\text{ker}(T)\in {\mathbb{R}}^m$.

In other words, the kernel of $T$ is the solution of the linear system:

$$A\vec{x}=\vec{0}$$

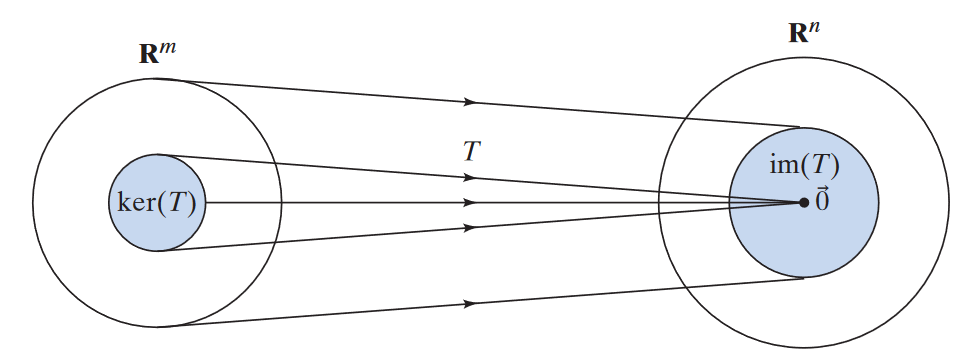If and only if $\text{ker}(T)=\vec{0}$, then we say the linear transformation is injective. The dimension of the kernel is the nullity of the matrix.

Solving by hand

For some matrix $A$:

$$A=\left[\begin{array}{ccccc}1& 2& 2& -5& 6\\ -1& -2& -1& 1& -2\\ 4& 8& 5& -8& 9\\ 3& 6& 1& 5& -7\end{array}\right]$$

We can perform row reduction to rref form:

See also

• Image
• Rank-nullity theorem