Image

The image (or column space) of a linear transformation is a subspace that is the set of values that the map results in its target space, i.e., for $T:{\mathbb{R}}^m\to {\mathbb{R}}^n$, the image is in the set of the codomain, $\text{im}(T)\in {\mathbb{R}}^n$.

More formally, we consider the image of a linear transformation as the span of a set of vectors, i.e., 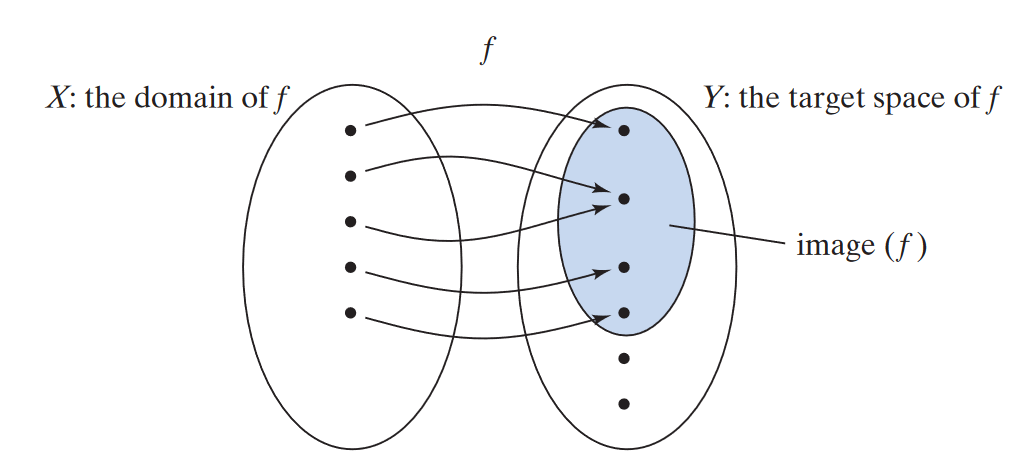$\text{span}(\overrightarrow{v_1},\dots ,\overrightarrow{v_m})$. If $\text{im}(T)={\mathbb{R}}^n$, then we say the map is surjective. Properties of subspaces are shared with images. The dimension of the image is the rank of the matrix, i.e., how many leading pivots a matrix has.

See also

• Kernel subspace
• Rank-nullity theorem
• Images, a page for a separate topic