Function (mathematics)

Functions form the base of much of mathematics. Functions with several independent variables and one dependent variable are multivariable. Functions with $n$ independent variables exist in ${\mathbb{R}}^{n+1}$.

Given two sets $A,B$, a function $f:A\to B$ is a map that takes an input in the domain $A$ and is associated with a single element in the codomain $B$.

Categories and types

Our common types are real-valued, vector-valued, and complex-valued functions.

In addition, many functions take the form of the below:

• Exponential function
• Logarithmic function
• Trigonometric function
• Hyperbolic function
• Unit step function

Important foundations

The set of possible function inputs is referred to as the domain of $f$. The set of possible outputs are referred to as the range (or codomain).

Functions (whether single-variable or multi-) must pass the vertical line test. No combination of inputs can result in more than one output.

Functions can be written explicitly (though not always):

$$y=f(x)$$ $$z=f(x,y)$$

Or in a more explicit form:

$$f(x,y,z)=0$$

We also commonly call functions scalar fields, since it returns a scalar value for every input position. The vector analogue of this is a vector field.

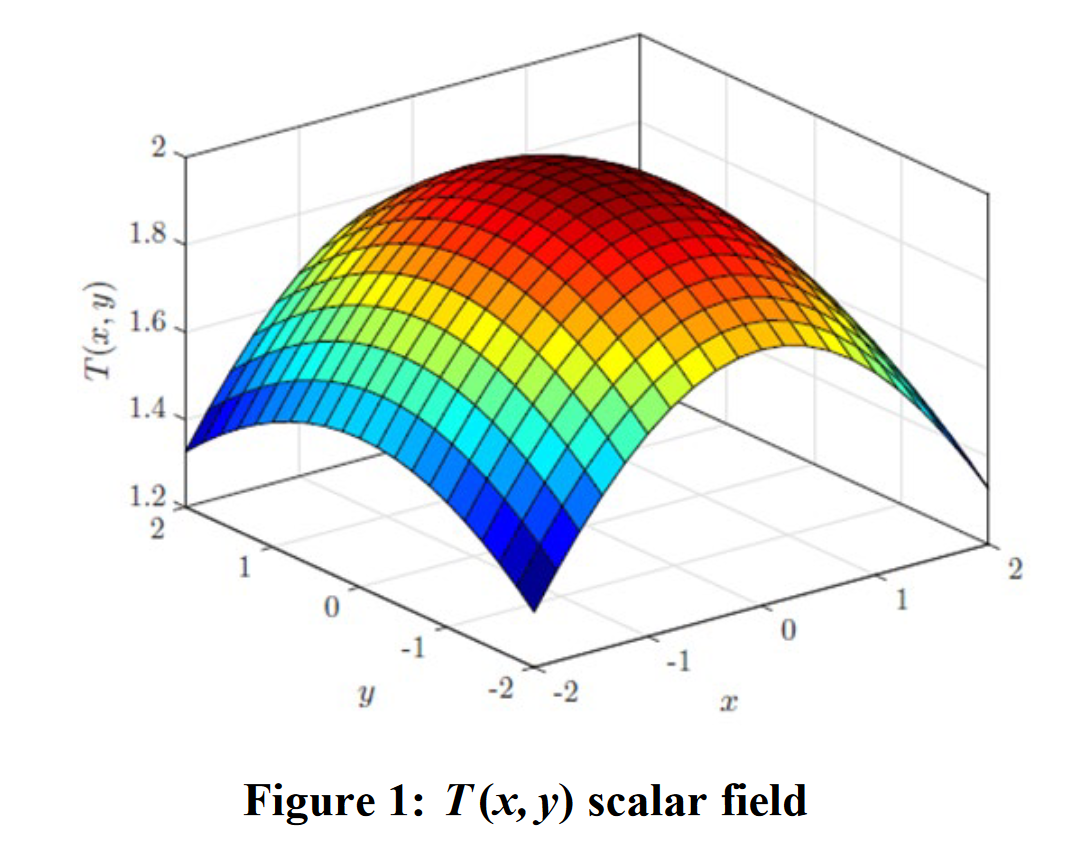
Computer solutions

We can use the Symbolic Math Toolbox in MATLAB to solve for functions at a particular value. This also works with complex solutions. For instance:

solve(t^2 + 6670 * t + 100000000 == 0, t)

See also

• For other uses, please see this page
• Graphing of functions