Linear approximation is the idea that we can approximate the value of a function with a tangent line at a point, if we zoom in sufficiently close. Then, for sufficiently close to , we can use . Linearisation is a useful technique in broad sub-fields of engineering, science, and mathematics. It’s the foundation behind small signal analysis.
We use the first-order Taylor series for this approximation, so the functions must be differentiable at the given point.
In multivariable calculus, we instead use the tangent plane, where we can approximate a curved surface by a plane that is tangent to the surface at the given point.
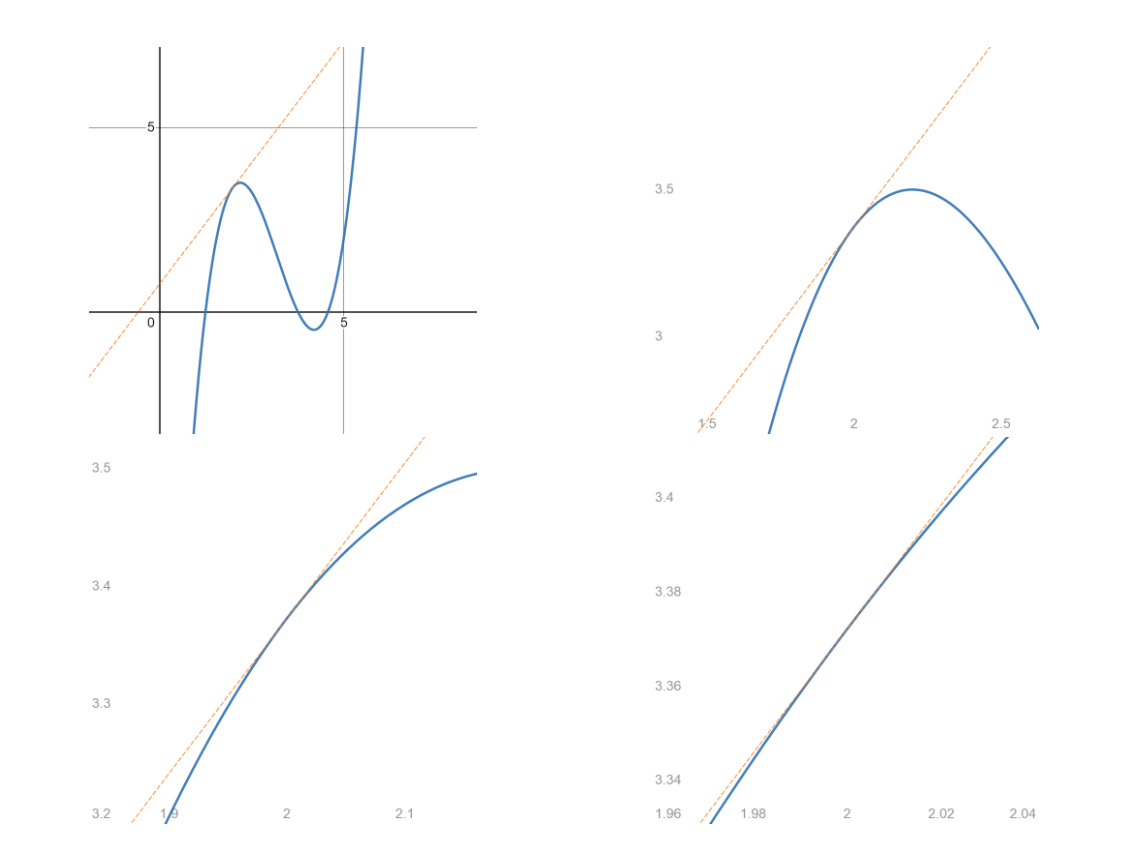
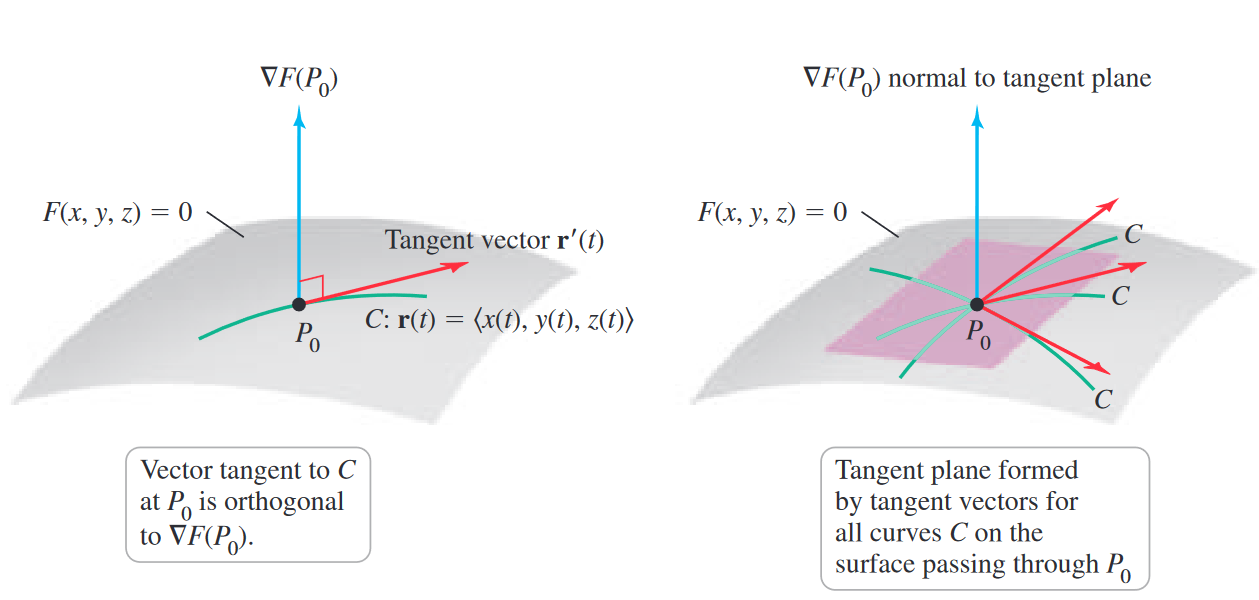
Common approximations
Trigonometric functions are approximated as: