The tangent plane extends the idea of linear approximations in two-dimensional space to higher-dimensional space. Specifically, for some function , we can approximate the curved surface at a given point by a plane that is tangent to the curved surface.
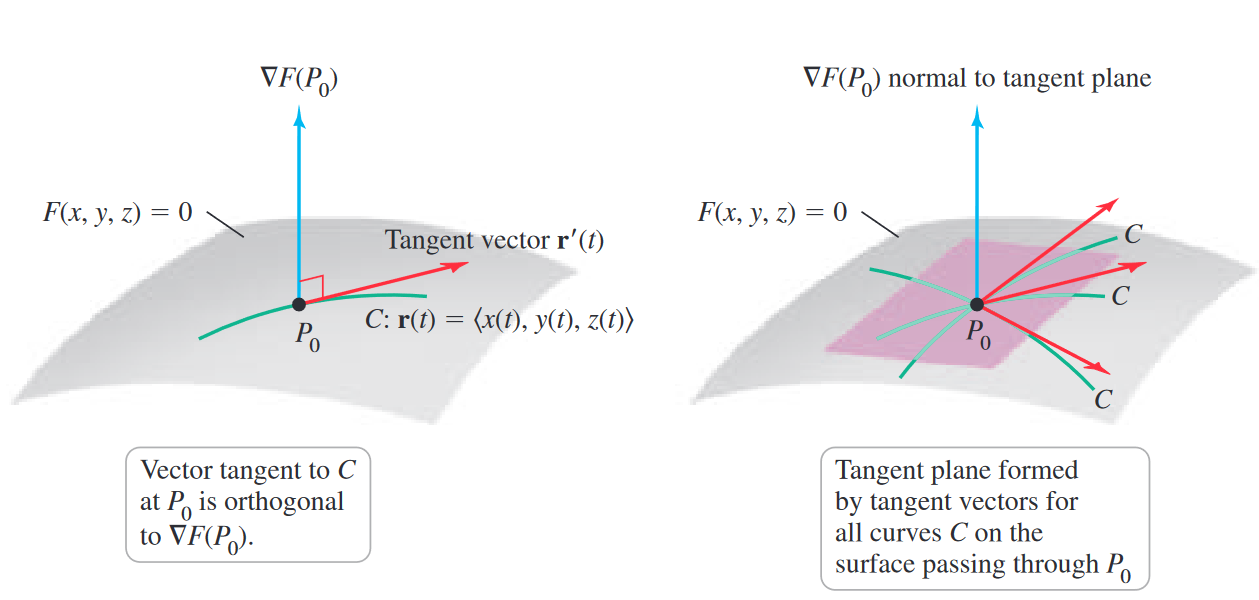The tangent plane for , where is differentiable at the point , is the plane passing through the point but orthogonal to . So we say the equation is:
Or alternatively using the gradient vector and the tangent vector :
For surfaces defined explicitly:
The equation of the tangent plane is:
Applications
We’re motivated to use approximations for applications in kinematics, geophysical problems, and time-independent models (where we can determine how sensitive the model is to small changes).
For instance, we can represent some differential change for the function with:
Derivation
We can take two approaches to derive. One is mainly geometric, the other involves the expansion of the Taylor series for a multivariable case. Anyways, this probably isn’t very important.
Our more intuitive derivation involves the Taylor series. We start with some explicit form instead with : then (alternatively the signs can be swapped). Eventually we can take the Taylor expansion for multiple variables (pretend all the partials are evaluated at ):
which can be expressed in a more compact form involving the Hessian matrix. There’s some more but I don’t feel like bringing it over here. Suffice to say we get a similar thing if we take the first-order Taylor series.
In the geometric case, we start with (in our particular case, we take ), i.e., we are plotting level surfaces. We take the following steps.
- For step 1, we prove that the level surface. If is 0, then they are perpendicular.
- Next, we determine the equation of the tangent plane. We fix some point as the reference point on the curved surface, choose some arbitrary point in space and create a vector between and , i.e., .
- Impose the condition of orthogonality between and and simplify whatever is the result, i.e., . So we get: