Limit

A limit is some value a function may approach (but not necessarily equal). In single-variable calculus, we define the limit of a single-variable function as follows:

We suppose the function $f(x)$ is defined for all $x$ near $a$ (but not necessarily $a$). If $f(x)$ is arbitrarily close to some value $L$ for all $x$ (but not necessarily $a$), then:

$$\underset{x\to a}{\lim }f(x)=L$$

Importantly! We can split limits up, including when we’re dealing with products and quotients.

Multivariable functions

The function $f$ will have the limit $L$ as $P(x,y)$ approaches some point $P_0(a,b)$. We use the delta-epsilon definition to define sufficient closeness.

$$\underset{(x,y)\to (a,b)}{\lim }f(x,y)=\underset{P\to P_0}{\lim }f(x,y)=L$$

For the multivariable case, it must approach $P_0$ along all possible paths in the domain of $f$.

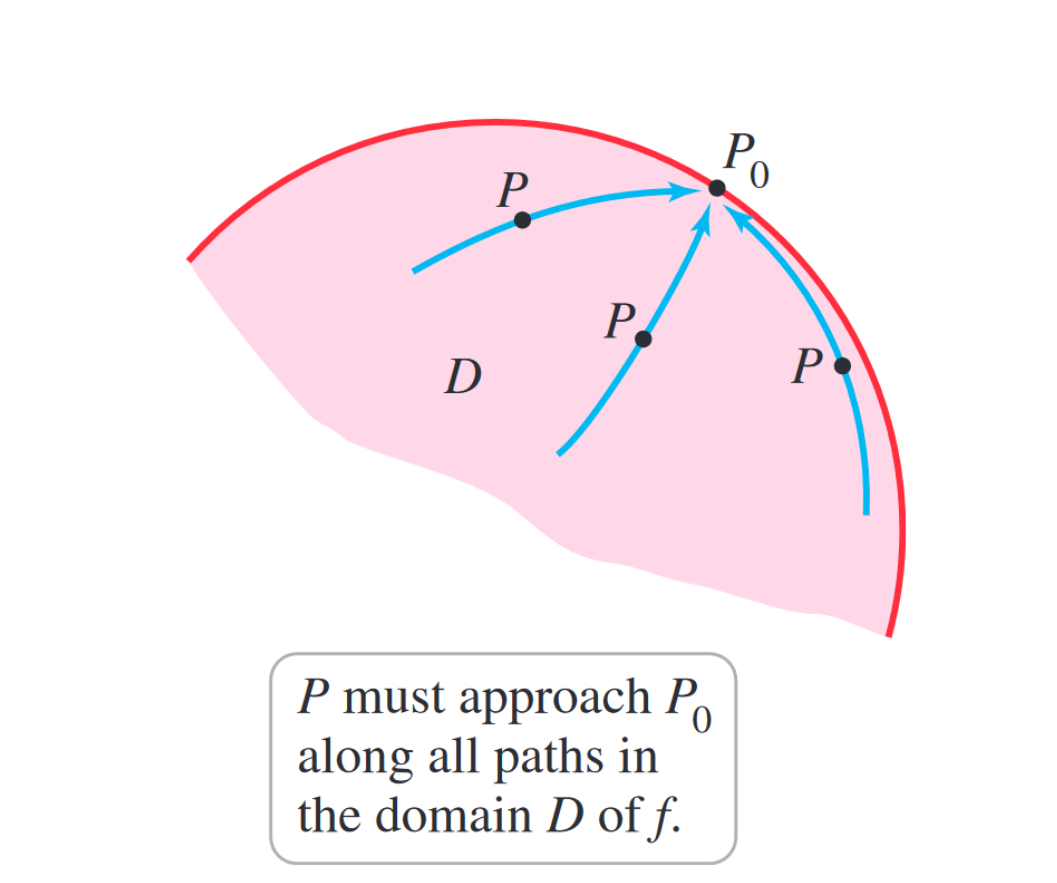
Existence and non-existence

We use delta-epsilon proofs to prove the (non)existence of limits, which can be tedious. For single-variable limits, good methods include factoring the numerator, multiplying by an algebraic conjugate, or the squeeze theorem.

The two-path test can also prove non-existence. If $f(x,y)$ approaches two different values as $(x,y)$ approaches $(a,b)$, then the limit does not exist, since it must approach along all paths in the domain. See that note for more details.

Key concepts

• Squeeze theorem, a classic proof method for the existence of limits
• L’Hôpital’s rule, for indeterminate limits
• Continuity, an extension of the notion of limits