Asymptotic notation

In computer science, asymptotic analysis describes how an algorithm scales with an input size that approaches infinity. There are three main types of notation: big-O, big-omega, and big-theta notation.

$O$-notation is the upper bound on an algorithm’s runtime. $\Omega$-notation is the lower bound. $\Theta$-notation (which is a tight upper/lower bound limit) describes precisely how the algorithm grows. For an informal guide to finding big-O, see the page for time complexity.

Formal definition

We describe the running time of algorithms in terms of functions that maps either from/to the set of natural numbers or the set of reals. $g(n)$ represents the bound on the number of operations that an algorithm takes. $f(n)$ is the function we’re analysing, which can be more complicated than $g(n)$. The running-time function is denoted $T(n)$. If a function $f$ belongs to the set of functions (let’s use big-O), we use a notational abuse to say that $f(n)=O(g(n))$.

This figure gives some intuition on where $n_0$ comes into play.¹ Essentially the value of $f(n)$ must be on or below $cg(n)$ for values to the right of $n_0$. We’re only interested in the long-term behaviour.

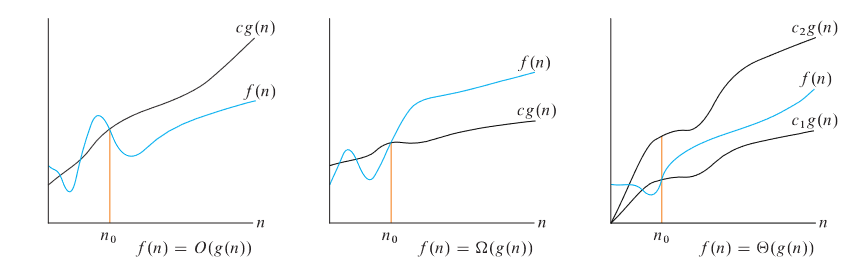
Big-O

For a given function $g(n)$, we denote $O(g(n))$ as the set of functions:

$$O(g(n))=\{f(n)|\exists c,n_0>0:0\le f(n)\le cg(n)\forall n\ge n_0\}$$

i.e., $f$ belongs to $O(g(n))$ if there exists a positive constant $c$ such that $f(n)\le cg(n)$. This definition requires that any $f\in O$ is asymptotically non-negative, i.e., for sufficiently large $n$, $f$ must be non-negative.

We also define little-O $o(g(n))$, which may not be an asymptotically tight upper bound.

Big-Ω

We denote $\Omega (g(n))$ as the set of functions:

$$\Omega (g(n))=\{f(n)|\exists c,n_0>0:0\le cg(n)\le f(n)\forall n\ge n_0\}$$

i.e., an asymptotic lower bound.

We also define little-omega $\omega (g(n))$, which may not be an asymptotically tight lower bound.

Big-Θ

We denote $\Theta (g(n))$ as the set of functions:

$$\Theta (g(n))=\{f(n)|\exists c_1,c_2,n_0>0:0\le c_{1}g(n)\le f(n)\le c_{2}g(n)\forall n\ge n_0\}$$

i.e., it was an asymptotically tight bound. By theorem, we have $f(n)=\Theta (g(n))$ if and only if $f(n)=O(g(n))=\Omega (g(n))$.

It’s usually a good idea to find $\Theta$ by proving big-O and big-Ω.

Properties

• If $f(n)=\Theta (g(n))$ and $g(n)=\Theta (h(n))$, then: $f(n)=\Theta (h(n))$.
• $f(n)=\Theta (g(n))$ if and only if $g(n)=\Theta (f(n))$.
• $f(n)=O(g(n))$ if and only if $g(n)=\Omega (f(n))$.
• $n^a\le O(n^b)$ if and only if $a\le b$.
• ${\log }_{a}n=O({\log }_{b}n),\forall a,b$.
• $c^n=O(d^n)$ if and only if $c\le d$.

Then, let $f(n)=O(f^{\prime }(n))$ and $g(n)=O(g^{\prime }(n))$, where the prime denotes an arbitrary function (not the derivative), then:

• $f(n)\cdot g(n)=O(f^{\prime }(n)\cdot g^{\prime }(n))$
• $f(n)+g(n)=O(\max (f(n),g(n)))$

Computations

Definitionally, we can prove the asymptotic bounds for functions, by making use of algebraic manipulations. This can be a little cryptic sometimes:

• For some compound expression, try to move $n$ out of the parentheses.

We can also easily compare the asymptotic bounds of multiple functions with the limit method and with L’Hôpital’s rule.

$$\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=0⟹f(n)=o(g(n))$$ $$\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}<\infty ⟹f(n)=O(g(n))$$ $$\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=\infty ⟹f(n)=\omega (g(n))$$ $$\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}>0⟹f(n)=\Omega (g(n))$$ $$\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=c,c\in (0,\infty )⟹f(n)=\Theta (g(n))$$

The logarithmic limit method supposes:

$$\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=L$$

Then, if we take the logarithm:

$$\underset{n\to \infty }{\lim }\left(\log \frac{f(n)}{g(n)}\right)=\log L$$ $$\underset{n\to \infty }{\lim }\frac{f(n)}{g(n)}=L=2^{{\lim }_{n\to \infty }\left(\log \frac{f(n)}{g(n)}\right)}$$

Practically, how do we use this? At step two, because we have a fraction, we expand out the logarithm to an algebraic expression with $\log$ in it. We take its result as the exponent for base 2. For $\infty$, we get $2^{\infty }=\infty$. For $-\infty$, we get $2^{-\infty }=0$.

Footnotes

1. From CLRS’ Introduction to Algorithms. ↩