Exponential function

Exponential functions, often denoted $\exp (x)$, involve raising $x$ to an exponent with $e$ as the base. Curiously its derivative and integral is the same function.

$$e^x=\exp x=\sum _{n=0}^{\infty }\frac{x^n}{n!}$$

Complex case

Exponential functions with complex inputs, i.e., $e^{x+iy}$ also have surprising properties.

$$e^z=e^{x+iy}=e^x(\cos y+i\sin y)$$ $$|e^{x+iy}|=e^x$$ $$\arg (e^{x+iy})=y+2n\pi$$

A complex exponent will have infinitely many values, because of the nature of the complex-valued logarithmic function.

$$a^z=e^{z\ln a}$$

Signal theory

Why do we care about complex exponential signals?

• They are building blocks for more complicated signals.
• They’re easy to manipulate, wrt to differentiation and integration.
• They simplify many formulas versus using $\sin$ and $\cos$.
• The frequency spectrum of such a signal is very simple; for a signal $e^{j{\omega }_{0}t}$, all energy is concentrated at a frequency ${\omega }_0$.

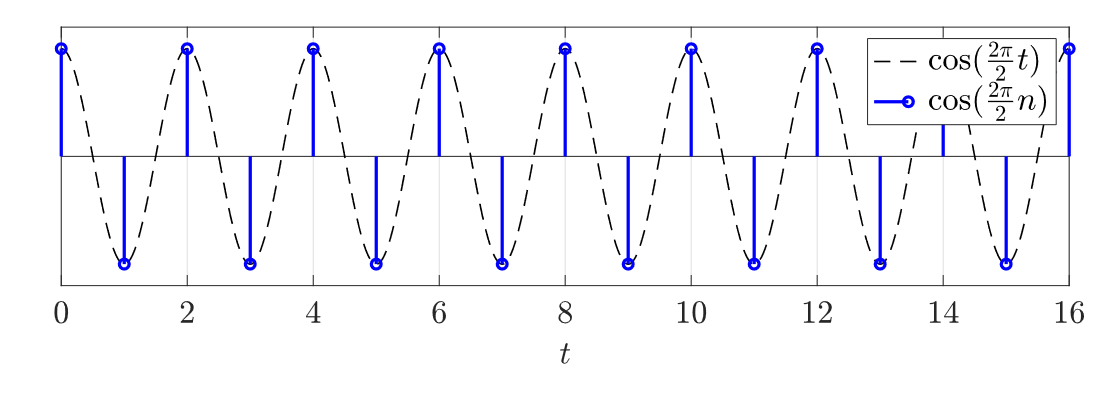
The DT case has a few important differences from the CT case. Depending on $\omega$, the DT signal can be periodic or aperiodic (with respect to time). If we drew out the unit circle on an Argand diagram, we may never reach the same point depending on what $\omega$ is (due to $\pi \notin \mathbb{Q}$).

If $\omega =k\frac{2\pi }{N},k\in \mathbb{Z}$ then the DT signal is periodic with respect to time.

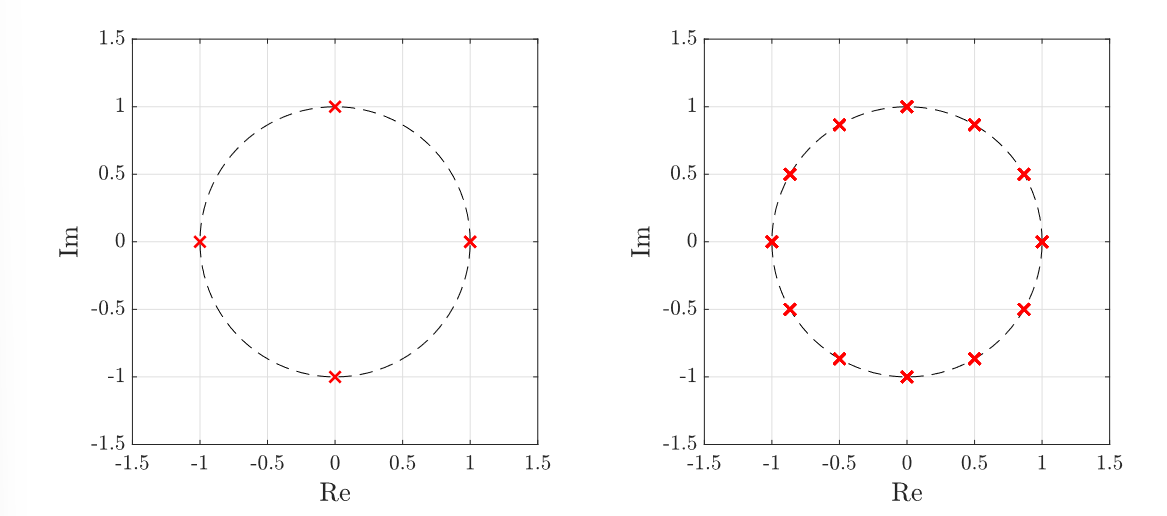For $\omega =\pi /2$ and $\omega =5\pi /6$: Note that it’s in fact periodic with respect to $\omega$:

$$e^{j(\omega +2\pi )n}=e^{j\omega n}{e}^{j2\pi n}=e^{j\omega n}$$

i.e., they’re periodic in frequency.

How do we tell if DT complex exponentials are periodic?

Find $N_0$ the usual way. If it’s a rational number, odds are that it’s actually periodic. The numerator is the fundamental period, the denominator is how many revolutions it takes for one cycle. Completely unintuitive.

When $\omega =\pi$, we get $e^{j\pi n}=(-1{)}^n$, i.e., it’ll jump back and forth between $\pm 1$, the fastest we can get in the DT case. A larger frequency doesn’t necessarily mean larger oscillations; oscillations will slow approaching an even multiple of $\pi$, and fasten at an odd multiple of $\pi$.

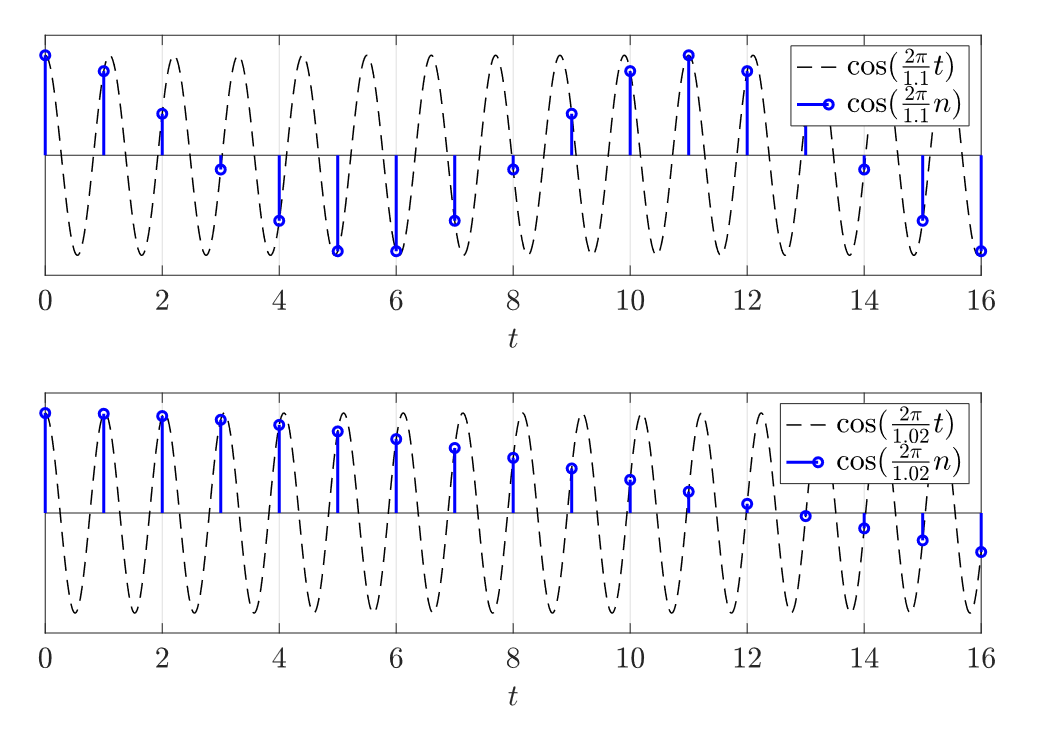
One important consequence of this is aliasing, since different frequency CT signals can produce the same looking DT signal.

By theorem, if $N_0\in \mathbb{N}$ is a desired period, then there are exactly $N_0$ distinct DT complex exponential signals of period $N_0$ given by:

$${\varphi }_k[n]=e^{jk{\omega }_{0}n};k\in \{0,1,\dots ,N_0-1\}$$

where ${\omega }_0=2\pi /N_0$. i.e., there are a finite set of “building blocks” when working with DT exponential signals.

A right-sided CT signal $x$ is of exponential class if $|x(t)|\le M{e}^{\sigma t}$ for some constants $M>0,\sigma \in \mathbb{R}$ and valid $\forall t\ge 0$. The smallest possible value for $\sigma$ is denoted ${\sigma }^{\star }(x)$. What this intuitively represents is our sharpest bound on the growth rate of $x$.

See also

• Logarithmic function