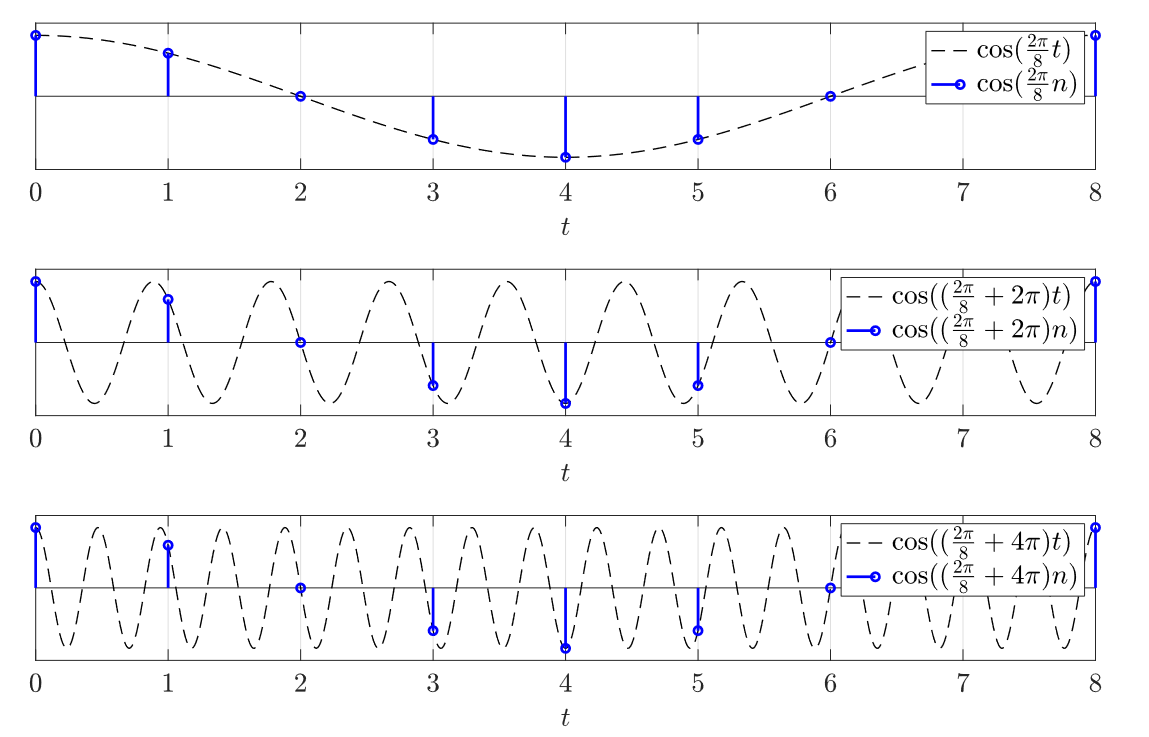
In signal processing, aliasing refers to the idea that different continuous-time signals can produce the exact same discrete-time signal when sampled. For sinusoidal signals, this is due to the properties of the complex exponential signal having a fastest period limit.
See the below for sampling period :1
This is especially relevant in image processing.
From the Nyquist-Shannon theorem, if our sampling rate is more than twice the bandwidth of the signal, we avoid aliasing. What happens if it’s less than twice the bandwidth and we want to recover the original signal?
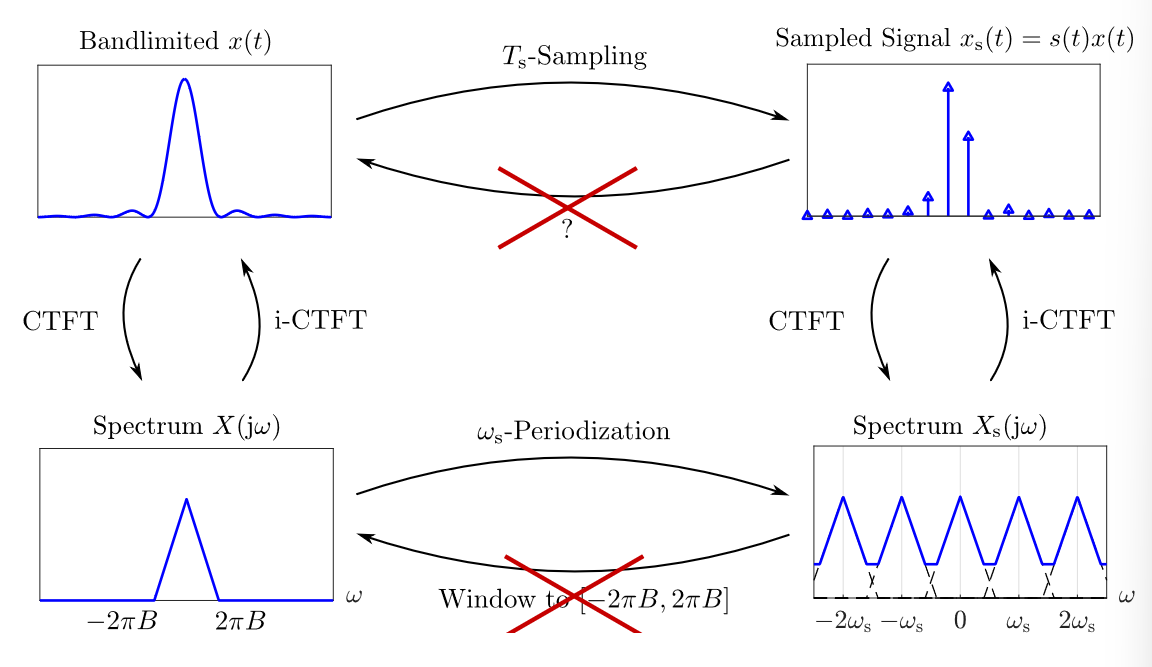i.e., the periodic spectrum is cut-off and we can’t uniquely recover the signal. If we take the inverse CTFT, we get a distorted version of the original signal, i.e., we get an aliased signal.
Spectrum
For an aliased signal, the signal will begin to overlap with itself. What does this mean?
To draw the spectrum of an aliased signal, draw it such that the extremities of each successive period overlaps. Then, only where it overlaps, take the algebraic sum.
Footnotes
-
From Prof Simpson-Porco’s lecture slides. ↩