Lebesgue space

In mathematics, Lebesgue spaces are vector spaces of functions, which find broad applications in signal theory. Common spaces for finite continuous-time signals include ${\mathsf{L}}_1$, ${\mathsf{L}}_2$, and ${\mathsf{L}}_{\infty }$ (and their discrete-time $l_i$ counterparts).

• If the action of a signal is finite, then we say $x\in {\mathsf{L}}_1$ (CT) and $x\in l_1$ (DT), i.e., it belongs to the space of Lebesgue integrable functions (CT) or the space of absolutely convergent sequences.
• If the energy of a signal is finite, then we say $x\in {\mathsf{L}}_2$ (CT) and $x\in l_2$ (DT), i.e., it belongs to the space of {square-integrable functions, summable sequences}.
• If the amplitude of a signal is finite, then we say $x\in {\mathsf{L}}_{\infty }$ (CT) and $x\in l_{\infty }$ (DT).

The signal spaces generally are defined as follows:

$${\mathsf{L}}_1=\{x:\mathbb{R}\to \mathbb{C}\mid \Vert x{\Vert }_1\text{is finite}\}$$

Relationships

The relationships between these common spaces are below, for CT and DT signals respectively.¹ 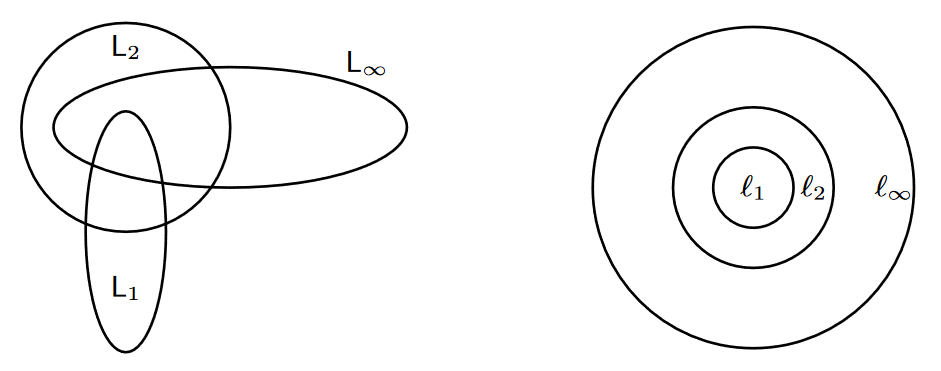The idea is that if $x\in {\mathsf{L}}_1\cap {\mathsf{L}}_{\infty }$, then it will also be $x\in {\mathsf{L}}_2$. This is provable (we try to find a bound on the energy):

$$\Vert x{\Vert }_2^2={\int }_{-\infty }^{\infty }|x(t){|}^{2}dt={\int }_{-\infty }^{\infty }|x(t)|\cdot |x(t)|dt$$ $$\le {\int }_{-\infty }^{\infty }(\underset{t\in \mathbb{R}}{\max }|x(t)|)\cdot |x(t)|dt=\Vert x{\Vert }_{\infty }\Vert x{\Vert }_1$$

With more computations of this type with varying signals we can discern the other relations.

For the discrete-time case, it’s much simpler to establish. We can say that if $x$ has finite energy, i.e.,:

$$\Vert x{\Vert }_2^2=\sum _{n=-\infty }^{\infty }|x[n]{|}^2$$

Then all the elements in the sum must too be finite. So $l_1\subset l_2\subset l_{\infty }$.

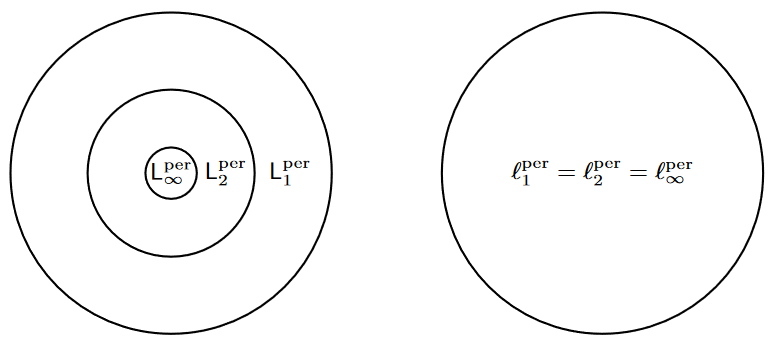
If the signal is periodic, the relationships simplify considerably. Signals of different types are useful for different purposes:

• ${\mathsf{L}}_1^{\text{per}}$ and $l^{\text{per}}$ are useful for the continuous-time Fourier series.
• ${\mathsf{L}}_1$ and $l_1$ are useful for the continuous-time Fourier transform.
• ${\mathsf{L}}_1$ and $l_1$ are useful for characterising bounded-input bounded-output (BIBO) stability of linear time-invariant (LTI) systems.
• ${\mathsf{L}}_{\infty }$ and $l_{\infty }$ are useful for describing signals in communications and control systems.

Footnotes

1. From Prof Simpson-Porco’s lecture slides. ↩