Fourier series convergence

The continuous-time Fourier series will converge under a specific set of conditions.

By theorem, if $x$ has finite action, $x\in {\mathsf{L}}_1^{\text{per}}$, then the Fourier coefficients ${\alpha }_k$ are well-defined and satisfy:

$$\underset{k\to \pm \infty }{\lim }|{\alpha }_k|=0$$

For an approximation ${\hat{x}}_K$, and an error function $e_K={\hat{x}}_K-x$, we say that ${\hat{x}}_K$ converges to $x$:

• Pointwise at $t_0\in \mathbb{R}$ if ${\lim }_{K\to \infty }{e}_K(t_0)=0$, i.e., for an infinite number of terms, there is no error.
• Uniformly if ${\lim }_{K\to \infty }\Vert e_K{\Vert }_{\infty }=0$, i.e., the amplitude of error goes to 0.
• In energy if ${\lim }_{K\to \infty }\Vert e_K{\Vert }_2^2=0$, i.e., the energy of the error goes to 0.

Then by theorem, if $x$ has finite action, we can deduce about ${\hat{x}}_K$‘s convergence:

• Pointwise convergence if we’re over time intervals where the signal is smooth.
• At a finite jump discontinuity, the approximation converges at the mid-point of the continuity.
  • This is why we can’t perfectly approximate square waves.
  • Called Gibb’s phenomenon.
  • We can’t represent jump discontinuities, since we basically have $\omega =\infty$ there.

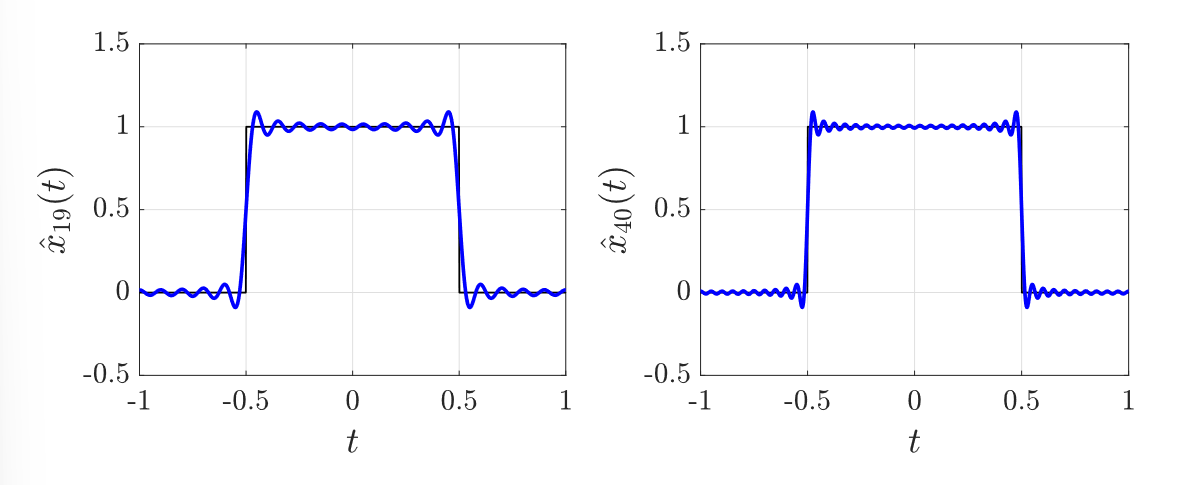
If $x$ has finite action, and if $x$ has a continuous derivative everywhere, then ${\hat{x}}_K$ converges to $x$ uniformly.

If $x$ has finite energy, $x\in {\mathsf{L}}_2^{\text{per}}$, then:

• ${\hat{x}}_K$ converges to $x$ in energy.
• The CTFS coefficients have finite energy, i.e., $\alpha \in l_2$.
• The signal and its coefficients will satisfy Parseval’s theorem.