Series convergence

Whether series converge or diverge is an important question in mathematics.

Infinite geometric series diverge if their common ratio $r<1$:

$$S_{\infty }=\frac{u_1}{1-r}$$

In the real case, we have an interval of convergence on the real number line. In the complex case, we have a disc of convergence. 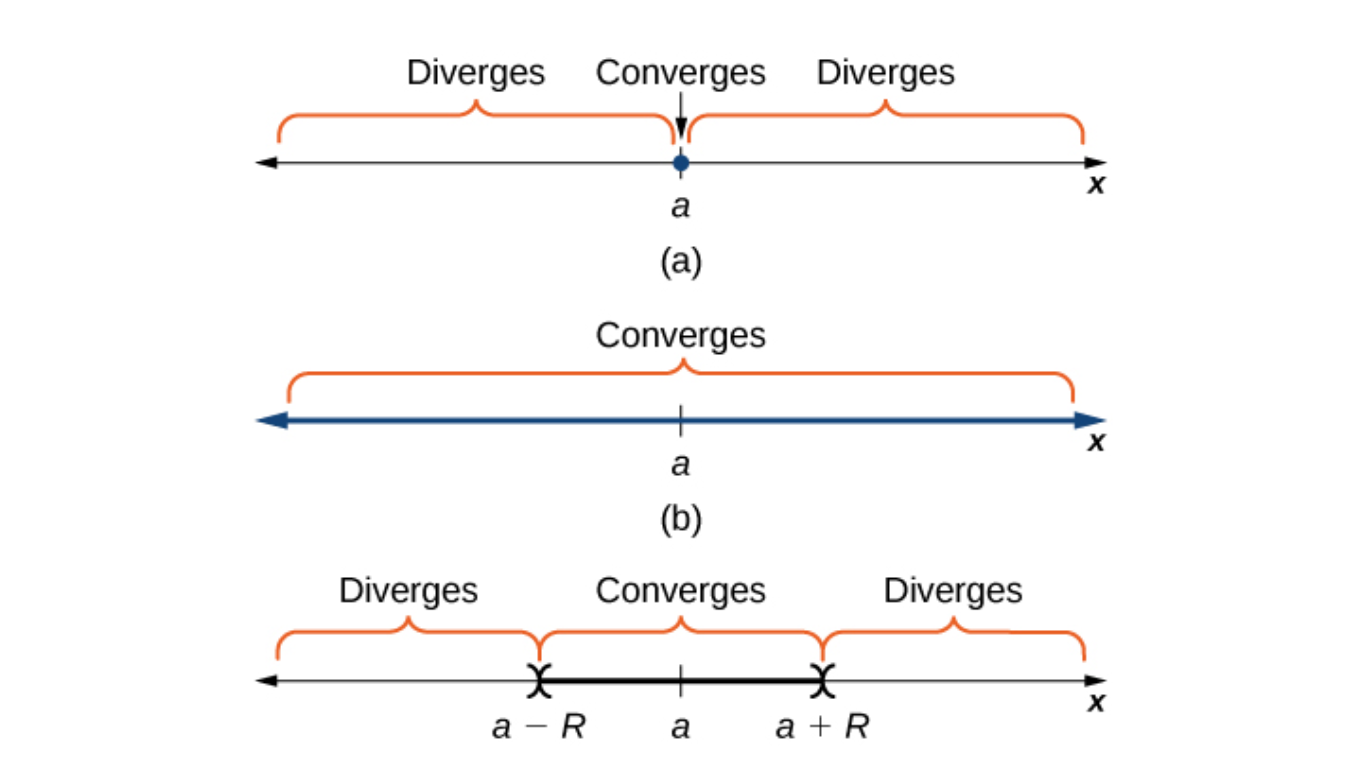By theorem, if ${\sum }_{n=1}^{\infty }{a}_n$ is such that ${\sum }_{n=1}^{\infty }|a_n|<\infty$, then ${\sum }_{n=1}^{\infty }{a}_n$ converges for $a_n\in \mathbb{C}$. In this case, we say the series converges absolutely. This is especially relevant for complex-valued $a_n$.

Finding radius of convergence

The ratio test is an intuitively easy way to test for convergence. We have a few more tools in the complex case.

Taylor’s theorem states that for any power series ${\sum }_{n=0}^{\infty }{a}_n(z-z_0{)}^n$, there is some $R\in [0,\infty ]$ such that the series converges absolutely for $|z-z_0|<R$ and diverges for $|z-z_0|>R$. In many cases, this is the quickest way to find the radius of convergence (since it’s pretty visual).