Ratio test

The ratio test is a way to determine whether a series (including power series) will converge or diverge.

If ${\sum }_{n=0}^{\infty }=a_n$ is a series with non-zero terms, then we define $\rho$:

$$\rho =\underset{n\to \infty }{\lim }\left|\frac{a_{n+1}}{a_n}\right|$$

• If $\rho <1$, then the series will converge.
• If $\rho >1$, then the series will diverge.
• If $\rho =1$, then the test is inconclusive and the series could be either.

Using $\rho <1$, we can determine a radius of convergence that we can guarantee the series will converge for. The interval for convergence is double the radius.

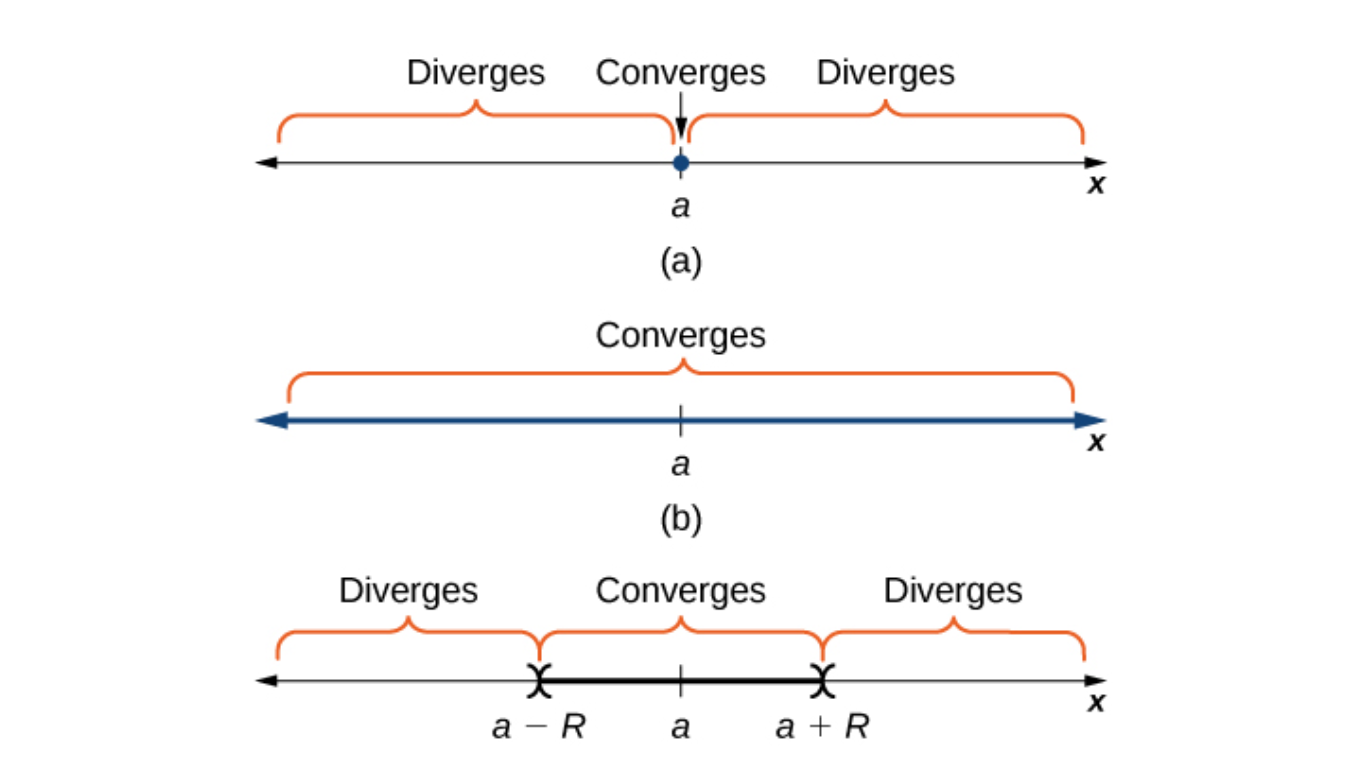
Complex-case

For complex-valued power series, we say:

$$\rho =\underset{n\to \infty }{\lim }\left|\frac{a_{n+1}}{a_n}\right||z-z_0|$$

If $a|z-z_0|<1$ then the power series converges. Compared to the real case, where we have an interval of convergence, in the complex case we have a disc of convergence.

Motivation

The intuition behind the ratio test comes from the idea that:

$$|a_{n+1}|=l|a_n|$$

for a very large $n$. And so on. We can roughly compare to a geometric series.

For the inconclusive case, we take a classic example:

$$\sum _{n=1}^{\infty }\frac{1}{n^2}\to \rho =1$$

which converges. But the following series diverges.

$$\sum _{n=1}^{\infty }\frac{1}{n}\to \rho =1$$

which is precisely why we need to find a different way to tackle the problem.