Finite state machine

Finite state machines (FSM, also finite state automata) are sequential circuits. As the name suggests, they have a finite number of states that the circuit operates in. We define several characteristics:

• A finite set of inputs (or alphabet) $\Sigma$.
• A finite set of states $Q$, with a designated initial state $q_s\in Q$.
  • A set of designated next states called the accepting states.
  • We also have a set of final or accepting states $F\subseteq Q$ — note that these don’t necessarily need to be terminal, but can proceed from this state if not finished. But the FSM can terminate here.
• A next-state or transition function $\delta :Q\times \Sigma \to Q$ that associates a next-state to a pair of current states/inputs. It is defined for all possible pair of states and inputs (it is a total function).
• In digital circuit design, we also have several features:
  • A set of flip-flops that help denote the next state $Y$ and current state $y$.
  • A set of outputs $z$.

FSMs find primary use in digital design as a control for systems that require responding to stimuli, including in processor design. Finite-state automata are themselves the subject of study in theoretical computer science, primarily in automata theory.

Our design procedure with FSMs is:

1. Draw the state diagram.
2. State table.
3. State code assignment.
4. State “assigned” table, i.e., a state table that uses binary state codes.
5. Derive logic functions for next state inputs and outputs.

Digital circuits

FSMs have a state at any given clock cycle. The next state ($Y_1,\cdots ,Y_k$) when a clock change occurs depends on inputs $w$ as well as the current state ($y_1,\cdots ,y_m$). Practical FSMs (especially in processor design) have two major components: a datapath and a control path. Combinational circuits are often used in conjunction with FSMs, often to encode or decode a signal.

There are two main types of FSM circuits. Moore FSMs have outputs that depend only on the state of the circuit. Mealy FSMs depend on the present state and inputs, and output on clock edges.

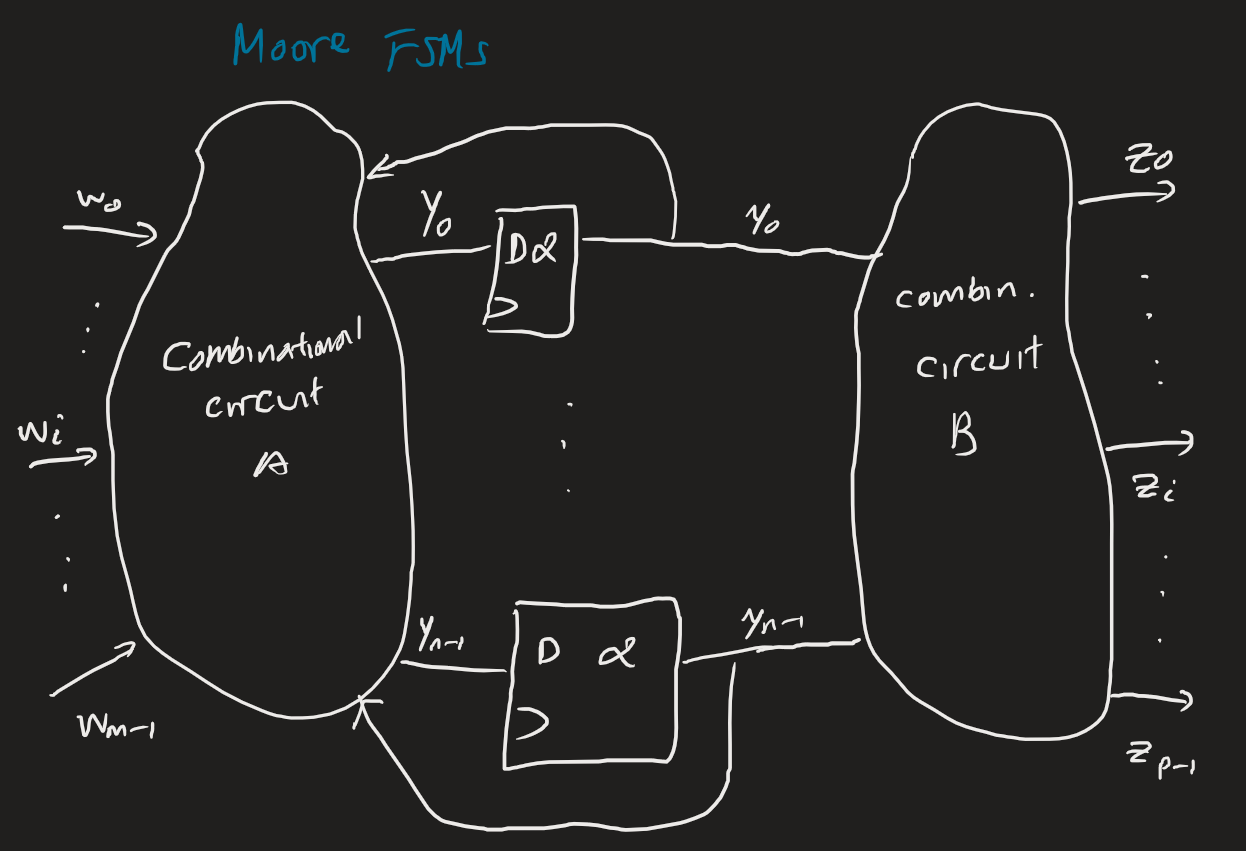
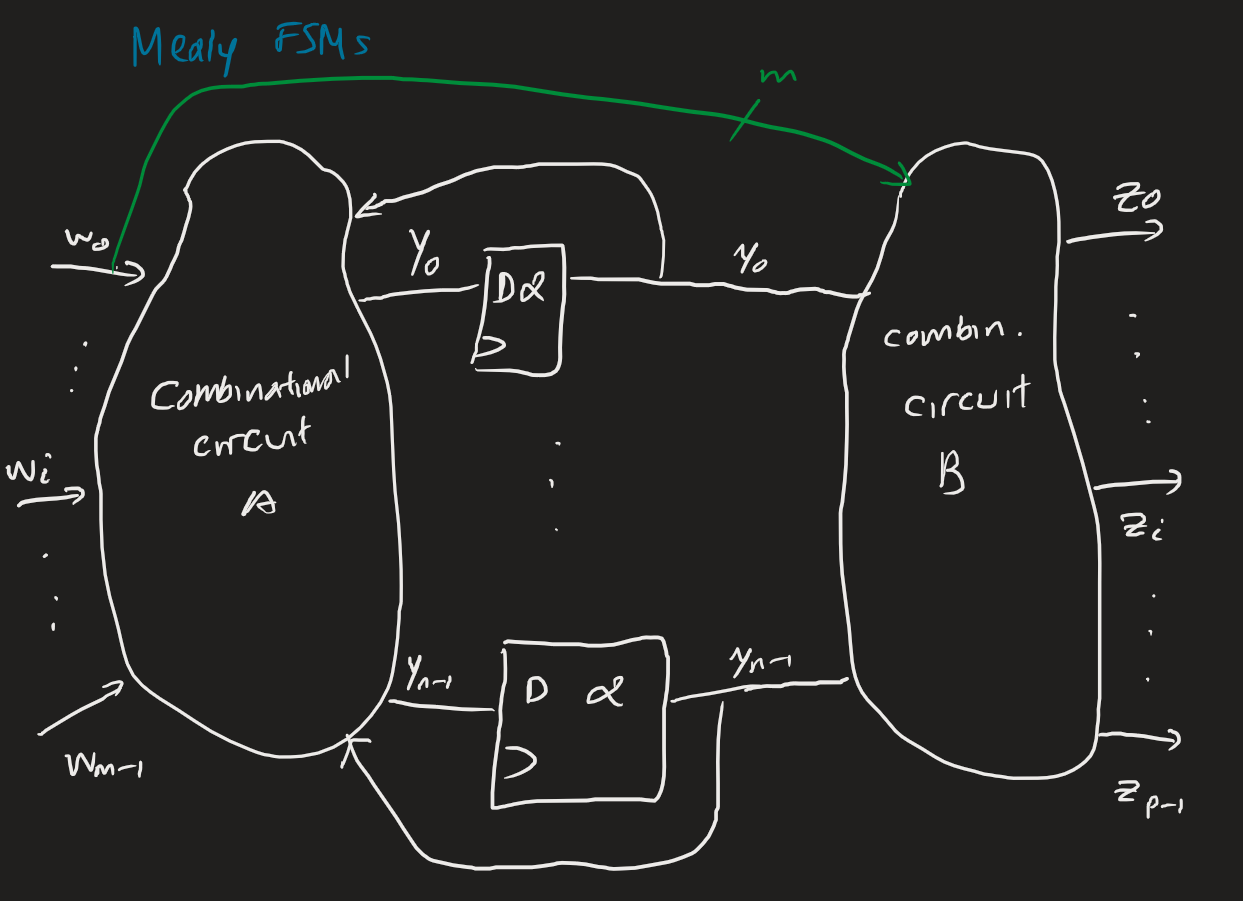
Automata theory

In automata theory, we divide our idea of FSMs into two types, deterministic finite automata (DFA) and non-deterministic finite automata (NFA). DFAs are special cases of NFAs.

• DFAs are exactly as we were discussing above,
  • Where there’s a unique transition (state diagram edge) for each state-input pair.
    • Strictly, we need total coverage of state transitions. We can introduce an error state that we can’t escape if we don’t have a valid encoding. This may be implicit!
  • The transition function is total.
  • Every transition requires an input. This is mainly because $ϵ$ transitions can make the FA non-deterministic.
• For NFAs, we relax these properties.
  • There can be multiple transitions, i.e., a single input may result in more than one transition. This means we have multiple paths to an accepting state, and not that there’s any inherent randomness. Just that we can take one transition, and if this doesn’t lead to an accepting state, take another available transition.
    • i.e., we encode alternatives
  • Not all transitions need to be specified.
  • Transitions with no input (i.e., the empty string $ϵ$) are possible.
    • No timing here. It’s just that given one state we can move to another. This is a mathematical expression.
  • The alphabet is also defined as the union with the empty string $ϵ$.
  • The transition function is now defined as $\delta :Q\times \Sigma \to 2^Q$. We map to the power set, which is the set of all possible subsets. This is because we can now transition to multiple output states on a single input state.
    • $\delta$ is no longer total, since we permit transitions on the empty string $ϵ$.

The language accepted by an FSM $A$ is the set $L(A)$ of all strings accepted by $A$. By Kleene’s theorem, for any formal language that is accepted by an FSM, there is a regular expression that defines the same language. The inverse case is true (for any regex, there is an FSM), provable with DFAs.

We can also convert NFAs to DFAs.

Visual representations

State diagrams give us an easy representation of what the next state could be for a given current state. The nodes denote states (and two concentric circles denote a final state), and the directed edges denote transitions. Markov chains are the probabilistic equivalent of finite automata — note how similar they look! 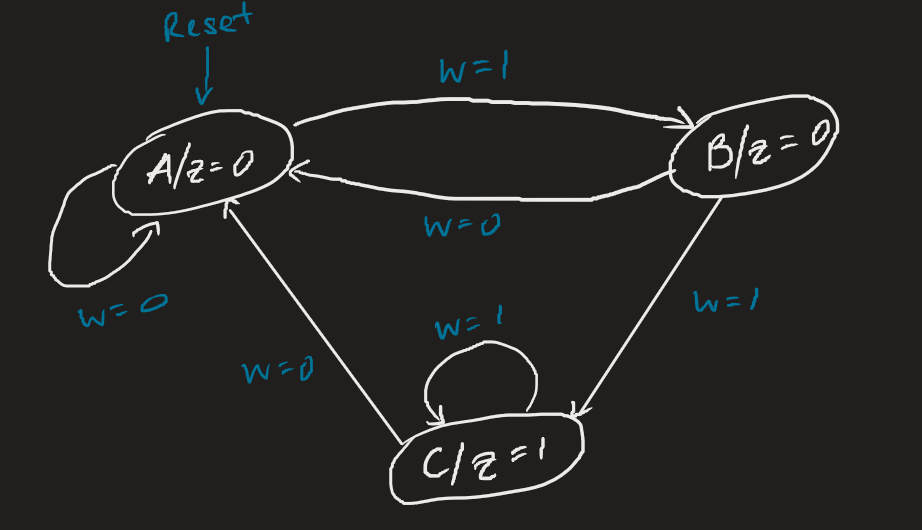And a state table encodes it in a more systematic way: 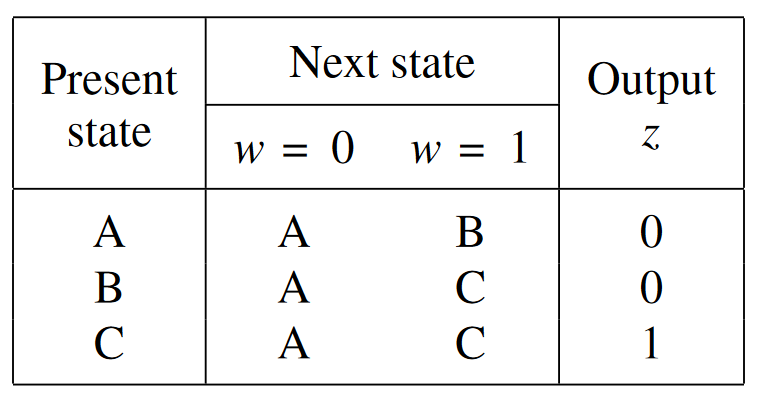We can generate state expressions $Y_0,\cdots ,Y_n$ using k-maps or alternatively with one-hot encoding.

State minimisation

todo