Markov chain

Markov chains describe stochastic processes. They are based primarily on states and transitions, where the probability of the next state depends only on the current state. Markov chains are essentially a probabilistic variant of finite state automata.

Fundamentals

Suppose we have three discrete states. Suppose also there is some probability that the state of one body either remains the same or changes to the two other states.

Some handy definitions:

• Probability vector: where the entries are non-negative and sum to 1
• Stochastic matrix (also transition matrices): where each column are probability vectors; $n$ by $n$*

When we apply some stochastic matrix $A$ to some distribution $\overrightarrow{x_i}$, our result describes the new distribution at state $t=i+1$. An interesting application examines our understanding of diagonalization, allowing us to explore the population as time approaches infinity. Recall that for some diagonalisable matrix, we can express it in terms of some matrix $V$, where its columns are eigenvectors and some diagonal matrix $D$, where its elements are eigenvalues.

$$A=VD{V}^{-1}$$

We apply it to our problem, using a handy theorem. If:

$$S^{-1}AS=B=\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_n\end{array}\right]$$

Then:

$$A^t=S{B}^t{S}^{-1}=S\left[\begin{array}{cccc}{\lambda }_1^t& 0& \cdots & 0\\ 0& {\lambda }_2^t& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_n^t\end{array}\right]S^{-1}$$ $$\underset{n\to \infty }{\lim }{A}^n=\underset{n\to \infty }{\lim }(VD{V}^{-1}{)}^n=\underset{n\to \infty }{\lim }V{D}^{n}V$$

This is substantially more computationally efficient — as opposed to $n$ number of computations, we instead do three. We refer to our resulting population as the equilibrium distribution for $A$.

$$\underset{n\to \infty }{\lim }(A^n\overrightarrow{x_0})=\overrightarrow{x_{equ}}$$

Example

Say we have three lecture sections and students are free to attend different lecture sections, with a probability of either staying in the lecture session they currently attend, or two probabilities of attending a different lecture section.

If we begin with some population $\overrightarrow{x_0}$:

$$\overrightarrow{x_0}=\left[\begin{array}{c}\frac{1}{3}\\ \frac{1}{3}\\ \frac{1}{3}\end{array}\right]$$

And some stochastic matrix that describes their behaviour after a state change is induced:

$$A=\left[\begin{array}{ccc}0.7& 0.1& 0.2\\ 0.2& 0.4& 0.2\\ 0.1& 0.5& 0.6\end{array}\right]$$

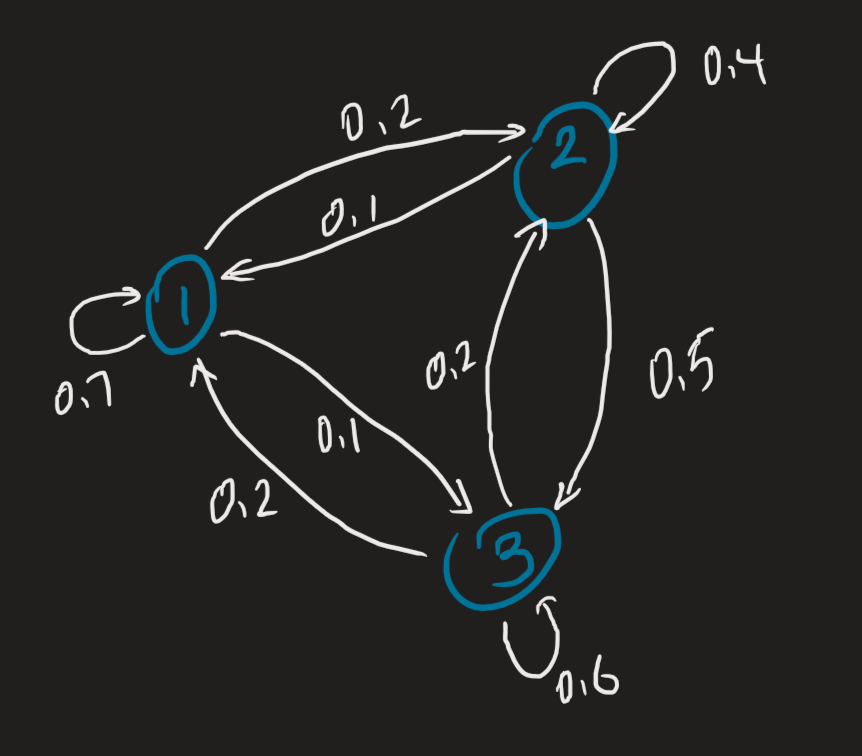
For the first column, 70% of students that are initially in the first lecture section will stay in that section. 20% will move to the second section, and 10% will move to the third section. We observe from above, that the vector $A\overrightarrow{x_0}$ describes the behaviour at $t=1$. We also observe that $A^n$ encodes the change between $t=0$ and $t=n$. Our understanding of diagonalization allows us to further extend this to find the number of students in each lecture section after an infinite amount of time.

Theorems

Equilibria for regular transition matrices Let $A$ be a stochastic matrix of size $n\times n$.

• There exists exactly one distribution vector $\vec{x}\in {\mathbb{R}}^n$ such that $A\vec{x}=\vec{x}$, i.e., that $\vec{x}$ is an eigenvector with eigenvalue 1. This is the equilibrium distribution for $A$, denoted $\overrightarrow{x_{equ}}$, which only has positive elements.
• If $\overrightarrow{x_0}$ is any distribution vector in ${\mathbb{R}}^n$, then ${\lim }_{n\to \infty }(A^n\overrightarrow{x_0})=\overrightarrow{x_{equ}}$.
• ${\lim }_{n\to \infty }{A}^n$ is a matrix whose columns are all $\overrightarrow{x_{equ}}$.