Karnaugh map

Karnaugh maps (or k-maps) are convenient alternatives to Boolean algebra simplification to minimise logic functions. They’re special “spatial” forms of truth tables where neighbouring cells differ in true/false value of one variable (not like truth tables). We essentially combine midterms.

In the two-variable k-map, we observe that regardless of the value of $x_1$ when multiplied together with $x_2$, we get true. Similarly for ${\bar{x}}_1$. We take that principle forwards.

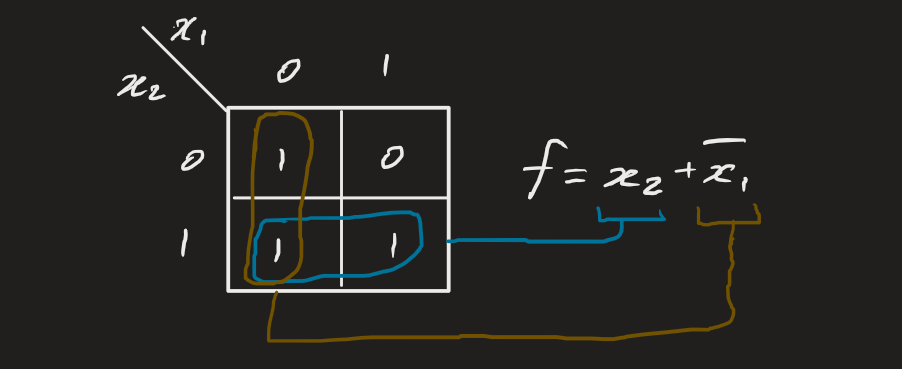
Construction

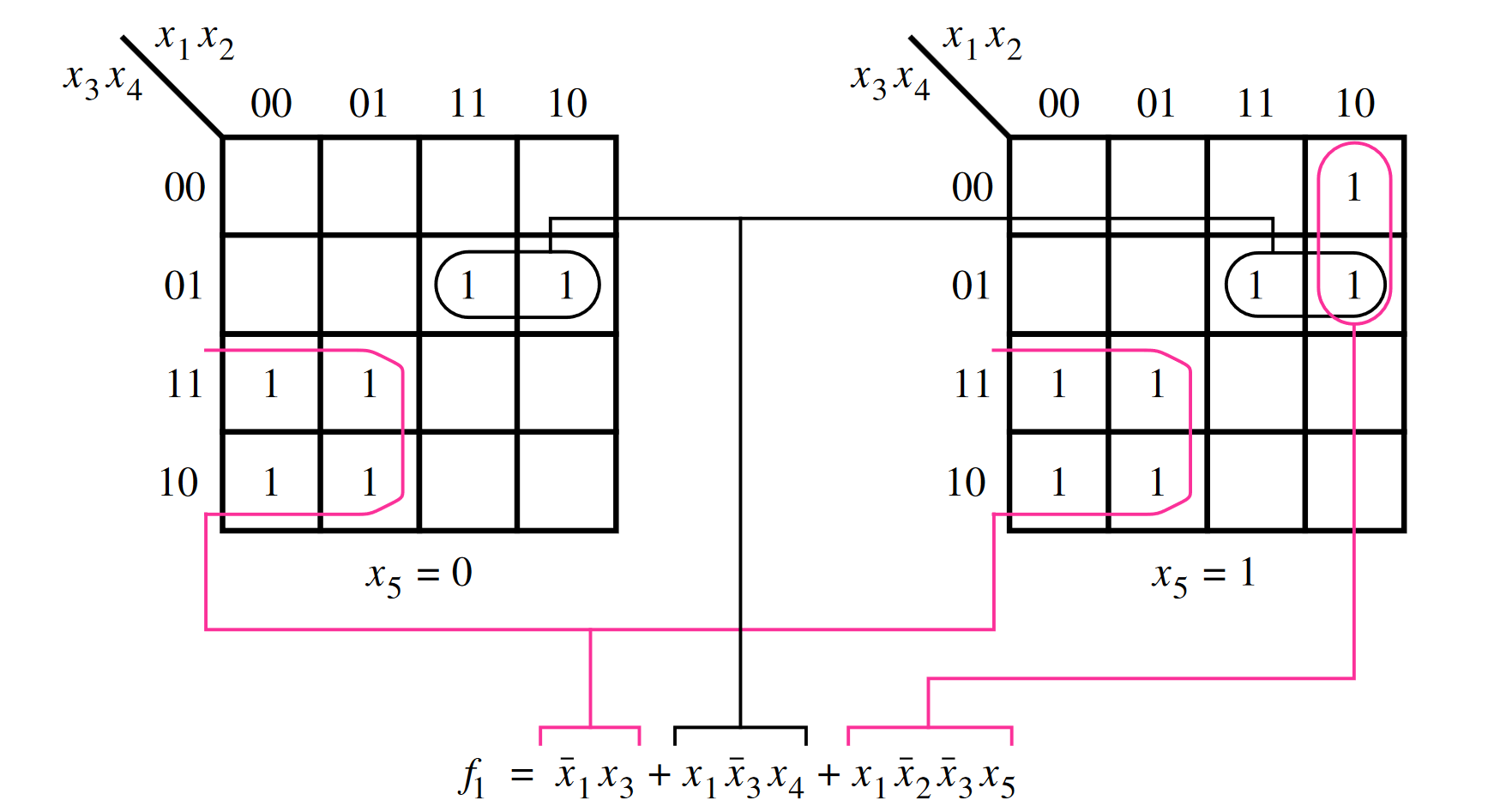
Higher-variable k-maps can be constructed by placing a group of variables on each axis. This is only really practical up to 4-variable maps. After this, with 5-variable maps it makes sense to build two separate maps where $x_5$ varies for each map.

Observe how the property above is maintained. Neighbouring axis cells only differ in the value of one variable until we cover every possible combination. Note also the order of minterms, starting from 0 at the top left and incrementing in the same column. 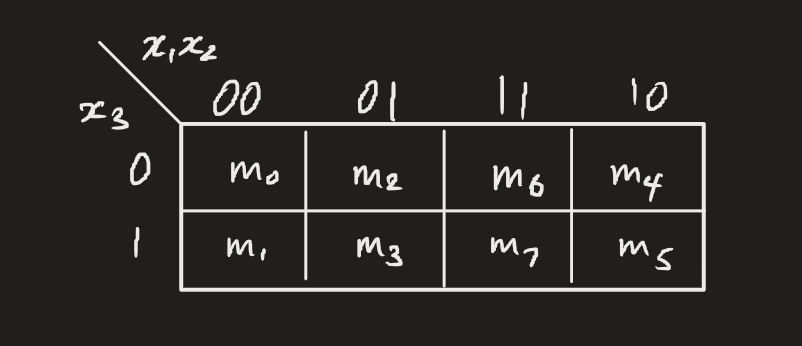Groups must be of a power of 2, and can extend off the table to the other end (like Pac-Man). Where there may be duplicate coverage, this means that there exists more than 1 minimal form. 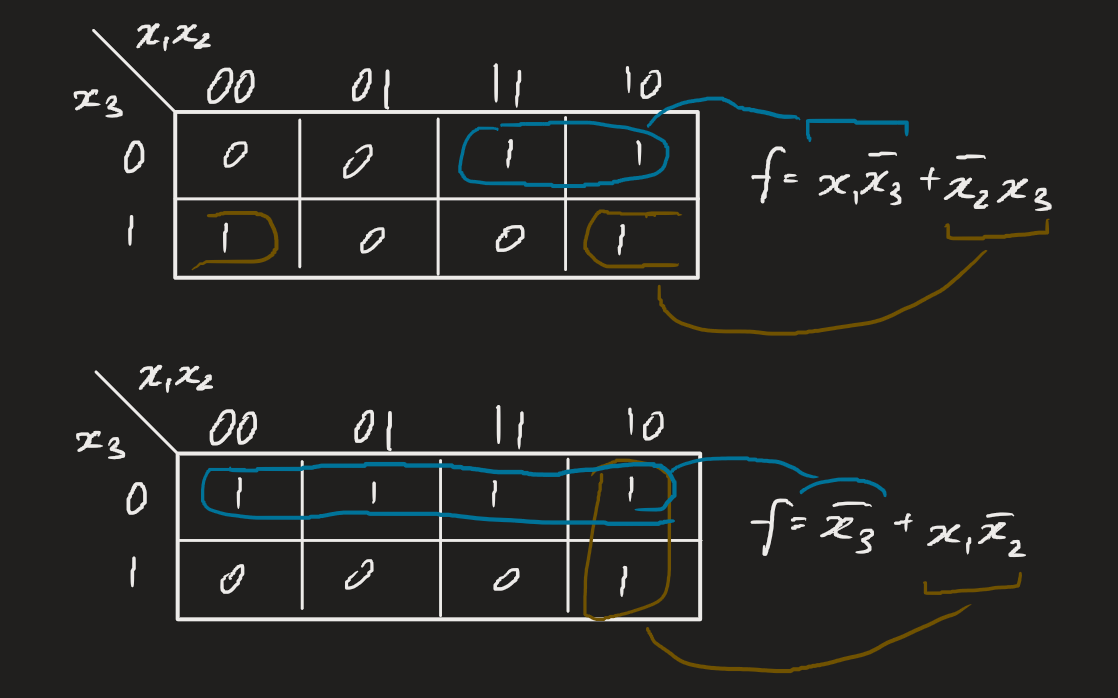Five-variable k-maps get pretty awkward. Extending k-maps beyond 5 variables isn’t really useful — mainly because CAD tools will perform necessary optimisation automatically.

Optimisation

We also define some key terms:

• Implicant: a product term for which a logic function evaluates to true. For example, for $f=x_1+{\bar{x}}_2{x}_3$, then both terms $x_1$ and ${\bar{x}}_2{x}_3$ are implicants.
  • Prime implicant (PI): product terms corresponding to the largest group of trues in the k-map.
  • Essential prime implicant: a PI that covers a 1-cell of a k-map that is not covered by any other PI
• Literal: a variable or its complement. In the above, the literals are $x_1,{\bar{x}}_2,x_3$.
• Cover: a set of product terms that “cover”, or include all the trues of a function.
  • Minimal cover: simplest logic expression that covers 1s in a k-map

Our minimisation steps involve:

1. Generate all prime implicants for $f$.
2. Find the set of essential prime implicants.
3. If the EPIs cover all valuations for which $f=1$, then we’re good. Otherwise, we add non-essential PIs until we get a minimal cover.

This seems pretty obvious.