Set theory

A set is an unordered collection of distinct objects, distinguished by its elements. For some element $a$ and some set $S$, we can say $a\in S$ if it is an element in the set. The empty set is denoted by $\varnothing$ or $\{\}$.

Basic definitions

We define some fairly common sets:

• $\mathbb{N}$, the set of natural numbers, i.e., positive integers including 0
• $\mathbb{Z}$, the set of integers
• $\mathbb{Q}$, the set of rational numbers, i.e., numbers that can be represented by fractions, $\frac{a}{b}$, where $a,b\in \mathbb{Z}$
• $\mathbb{R}$, the set of real numbers (or scalars)
• $\mathbb{C}$, the set of complex numbers
• $\mathbb{F}$, notation for either $\mathbb{R}$ or $\mathbb{C}$ (from the idea of fields)

Using set builder notation, we sometimes define a set by a given condition.

$$E=\{x\in S\mid P(x)\}$$

for some logical predicate $P(x)$ that holds true if an element is in the set.

We say that $A$ is a subset of $B$ if all the elements of $A$ are in $B$. In other words, $A\subseteq B$ if for every $a\in A$, $b\in B$. We also say that $A$ is equal to $B$ if $A\subseteq B$ and $B\subseteq A$. If $A\ne B$, then we say $A\subset B$.

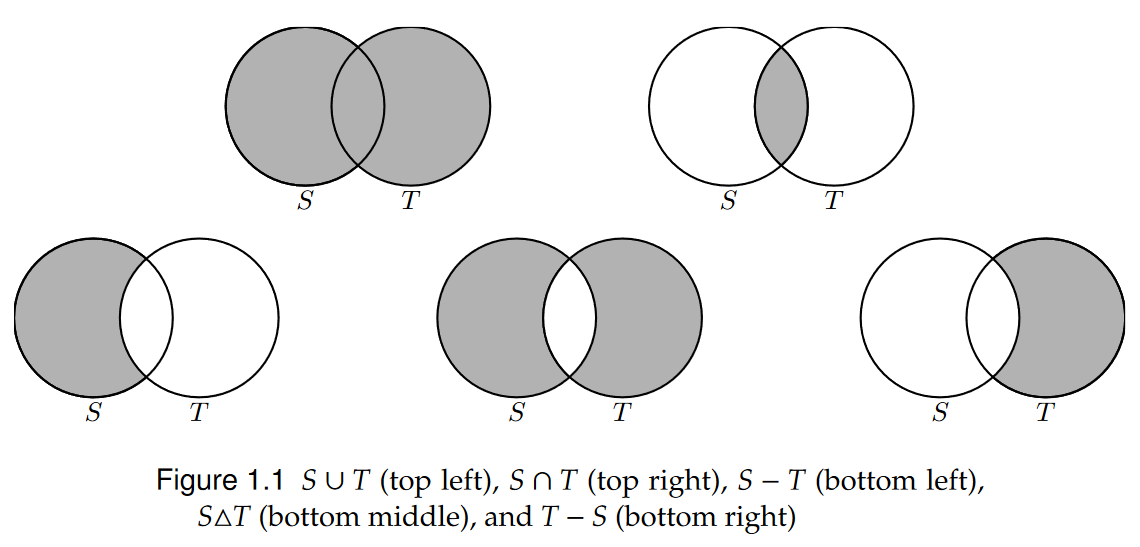
Additionally, we define the union and intersection of sets with $\cup$ and $\cap$, respectively. The union describes the set of all elements belonging to both sets, and the intersection describes the set of all common elements of both sets. See the below for their respective representations:

$$S\cup T=\{x:x\in S\text{OR}x\in T\}=\{x:(x\in S)\vee (x\in T)\}$$ $$S\cap T=\{x:x\in S\text{AND}x\in T\}=\{x:(x\in S)\wedge (x\in T)\}$$

Both the intersection and union are commutative, associative, and distributive. This generalises to multiple sets. We denote ${\cup }_{S\in \mathcal{S}}S$ as the union of all sets $S\in \mathcal{S}$, and ${\cap }_{S\in \mathcal{S}}S$ as the intersection of all sets $S\in \mathcal{S}$.

We define the relative complement of $T$ in $S$ as:

$$S-T=\{x\in S\mid x\notin T\}$$

This doesn’t require $T$ to be a subset of $S$. If $T\subseteq S$, then we define the absolute complement of $T$ in $S$ as:

$$S\backslash T=\{x\in S\mid x\notin T\}\approx S-T$$

The symmetric complement is the set:

$$S\Delta T=(S-T)\cup (T-S)=T\Delta S$$

Less basic definitions

For a set $S$, an unordered pair is any subset of $S$ with two elements. The collection of unordered pairs in $S$ is denoted by $S^{(2)}$. For any subset with $k$ elements, we denote its collection $S^{(k)}$ called the set of unordered k-tuples. An ordered pair of $x\in S$ and $y\in T$ is the set $(x,y)=\{\{x\},\{x,y\}\}$.

The Cartesian product of $S$ and $T$ is the set:

$$S\times T=\{(x,y)\mid x\in S,y\in T\}$$

i.e., the elements of the product form an ordered tuple. As a more concrete example, ${\mathbb{R}}^3$ is a Cartesian product of $\mathbb{R}\times \mathbb{R}\times \mathbb{R}$.

Disjoint sets are sets with no element in common, i.e.,:

$$A\cap B=\varnothing$$

If multiple disjoint sets $B_1,\cdots ,B_n$ whose union equals a set $S$, then these sets are a partition of $S$.

$$S=B_1\cup \cdots \cup B_n$$

The cardinality of a set refers to its size. For a finite set, the cardinality can be quantified with a natural number, which facilitates comparing the cardinalities of different sets.

More definitions

The successor of $S$ is the set:

$$S^{+}=S\cup \{S\}$$

i.e., the successor is a set whose elements are the elements of $S$ and an additional element: the set $S$ itself. This allows us to rigorously construct the natural numbers.

For a set $A$, the power set $P(A)$ refers to the collection of all subsets of $A$. $P(A)$ is itself a set whose elements are the different possible subsets of $A$.

Sub-pages

• Relations
• Maps
• Graph theory