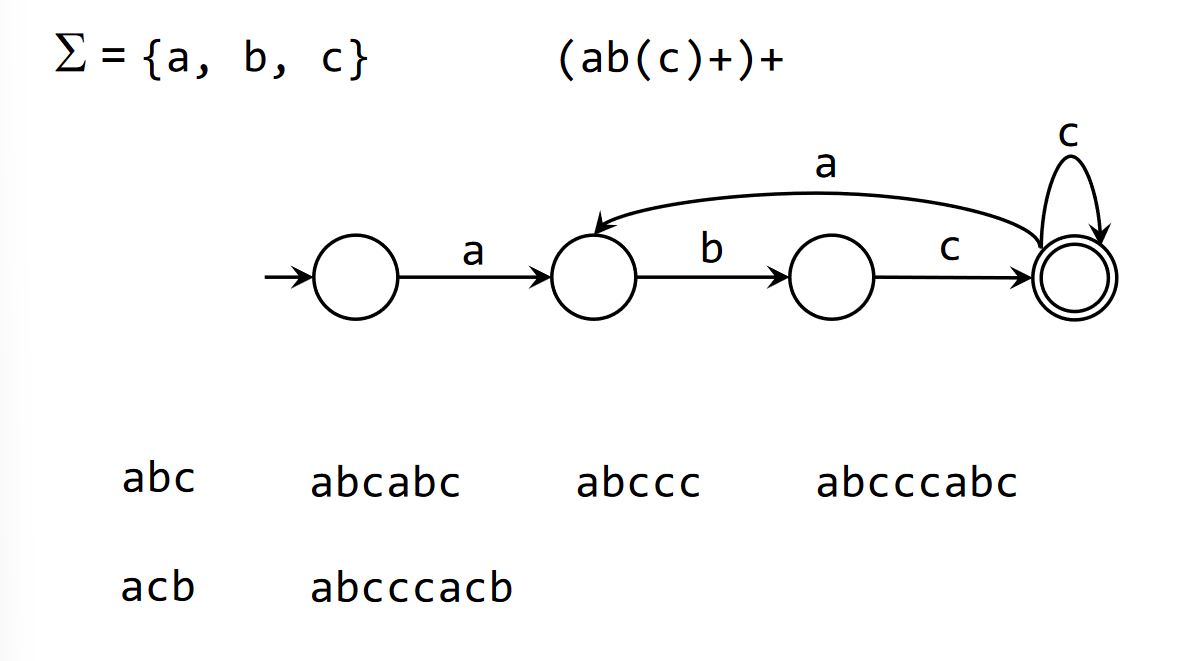
In computer science, a regular expression (regex) is a method to define a formal language. Practically speaking, regex is used in software engineering to define a description of a pattern of text to search for. Formally, we use a recursive definition to define the following regular expressions over an alphabet :1
- Base: (empty set), (empty string), and each symbol individually in are regular expressions over .
- Recursion: if and are regular expressions over , then , , and (i.e., concatenation, alternation, or the Kleene closure) are also regular expressions over .
- The “recursion” here comes from the idea that any more “complicated” regex can be recursively broken down into base operators one-by-one, observing their precedence.
- Then, we can define the Kleene closure given a regex with: .
- Restriction: nothing except for the above are regular expressions over .
Given a finite alphabet, the set of sentences obtained by a regular expression defines a formal language that is generated/accepted by , denoted .
Every regular expression over the alphabet defines a formal language.
The basics
Remember our basic formal language operators. In order of precedence:
- Set of characters: denoted with square brackets (i.e.,
[a, z]) - Grouping/scoping: denoted with parentheses.
- Repetition:
- Kleene closure:
*, which denotes zero or more instances of the substring. +, which denotes at least one or more instances.b+ == bb*
- Kleene closure:
- Concatenation: substrings next to each other.
- Alternation (logical OR):
|vertical pipe.
From here, we can construct any valid regular language. Many regex utilities allow the use of
Finite automata
Finite state automata are able to recognise sentences specified by a regex. By Kleene’s theorem, for any formal language that is accepted by an FSM, there is a regular expression that defines the same language. The inverse case is true (for any regex, there is an FSM), provable with DFAs.
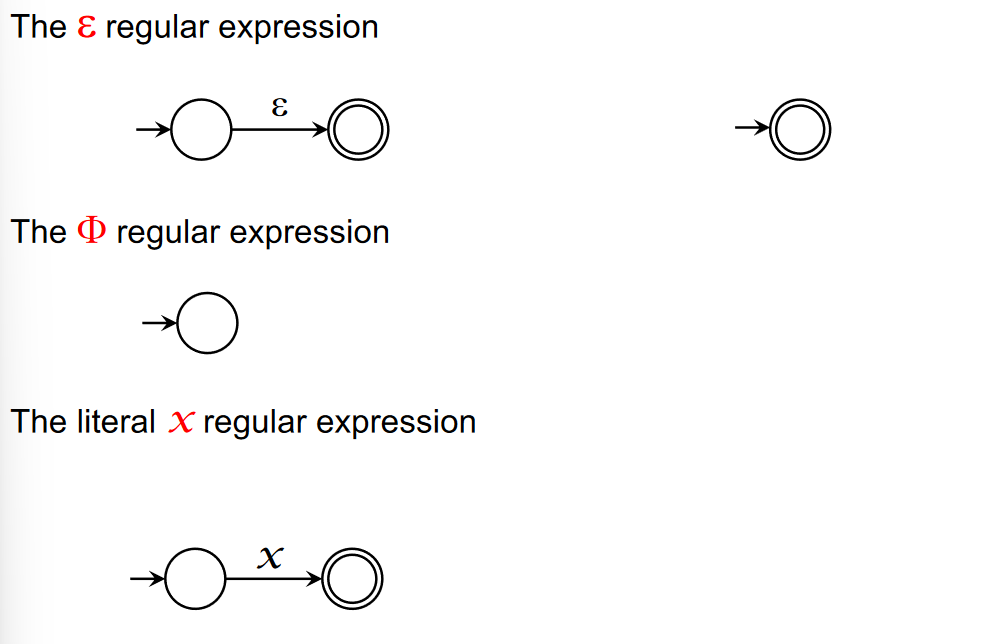
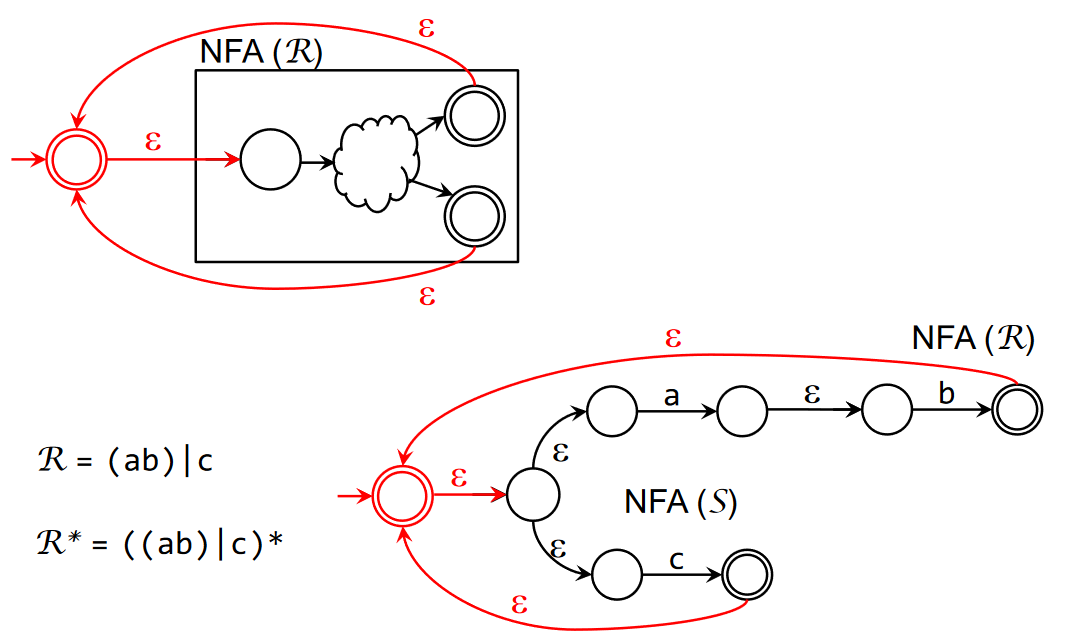
 All the fundamental regex operators can be converted to an NFA. These conversion rules are systematic, but don’t necessarily result in the smallest possible NFA (mainly because of the inclusion of the transition).
All the fundamental regex operators can be converted to an NFA. These conversion rules are systematic, but don’t necessarily result in the smallest possible NFA (mainly because of the inclusion of the transition).
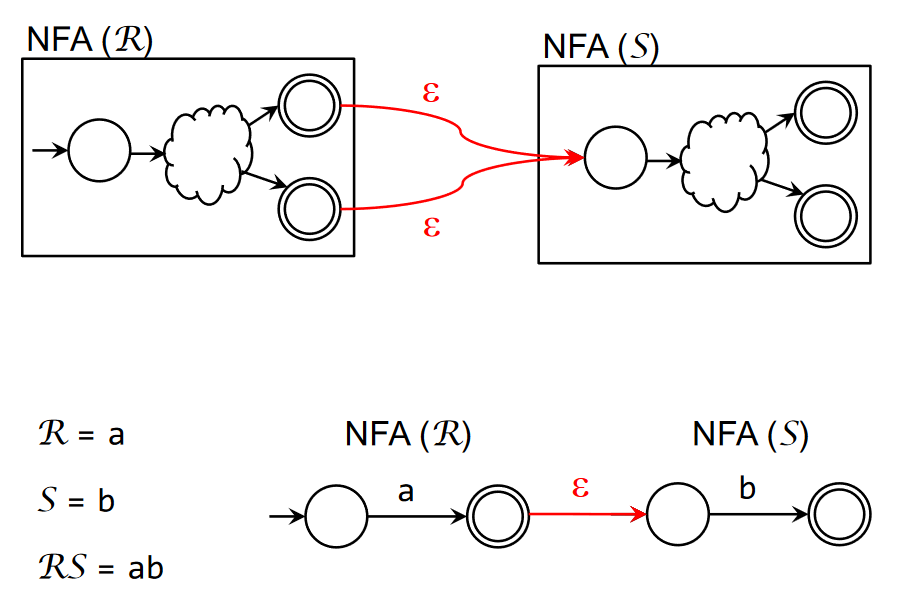
 For the concatenation operator. The intermediate accepting state becomes a regular state.
For the concatenation operator. The intermediate accepting state becomes a regular state.
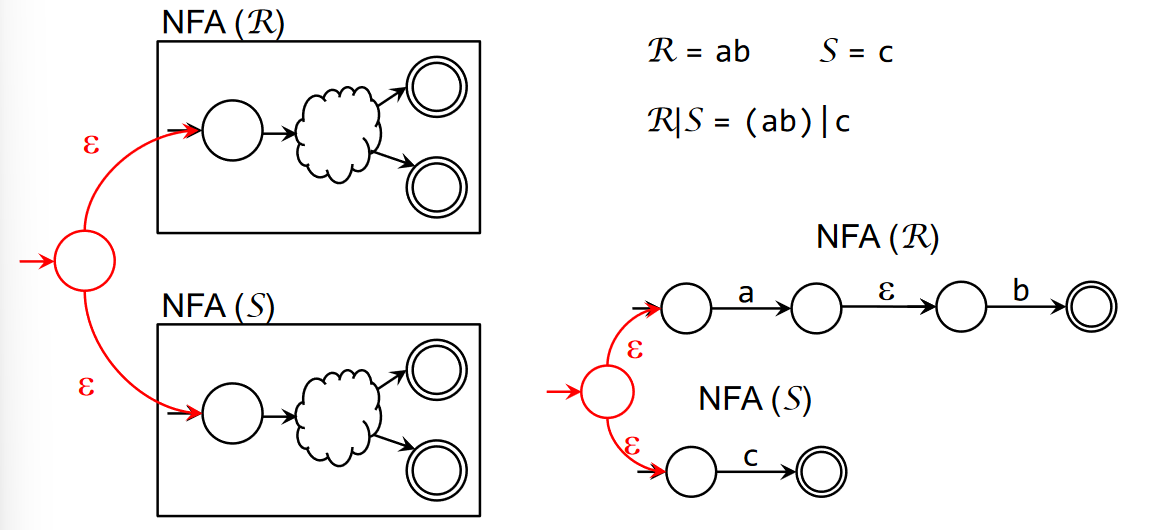
 The alternation operator:
The alternation operator:
 And the Kleene closure:
And the Kleene closure:
Applications
Note that commercial regex engines usually use a backtracking algorithm that runs in time. This is mainly because constructing a corresponding DFA for complex expressions can be prohibitively expensive.
Note also that backreferences, i.e., a regular expression that searches for things like <a> content </a>, where it matches on <a> then matches on </a> cannot be described by a regular language (since finite automata have no memory). This means (among other things) that XML and HTML matchers cannot be implemented efficiently.
Language-specific
In Rust
We can rely on the regex crate.
Footnotes
-
From Discrete Mathematics with Applications, by Susanna Epp. ↩