Recursion

Recursion is a general problem-solving approach that premises that we break a problem down into smaller versions of the same problem, until we can’t break the problem further (a base case). After this, we combine solutions to smaller problems to form the solution to the original problem. Recursion lends itself really well to induction.

In programming, we think about this as a function calling itself, but where the work done in each recursive call becomes smaller. We must have a terminating condition (or a base case), which is a condition where we end the recursion (and have reached maximum depth). In terms of memory, each function call has its own place in the stack (with its own local variables).

Within our function calls, whenever we have a return statement, it returns to the function call before it, not immediately to main. Note that we aren’t restricted to returning a value right away — we can do some operations then do the next recursive call.

Mathematically, recursive functions are expressed using recurrence relations.

High-level

There are three rules we must obey in recursion:

• Base cases must be correct.
• Recursive calls must shrink to a base case.
• Assume recursive calls are correct.

To tackle recursion problems, we first start with the recurrence relation. We have to define the base case, any actions we take (more recursive calls), consequences (transitions), contributions (return values), and affected variables (parameters). Some more ideas:

• We shouldn’t think more than 1 recurrence down. Think about a $k$-th case, and no more than that. As in induction, we assume the $k$-th case is correct if the base case is correct.
• We should name a function on what it promises to do.
• Don’t print or simulate anything. This costs time and can be painful. Just read things out loud.

Implications

Python is “comparatively slow” at recursion and has a limited stack depth.¹ The reason this is the case is because it lacks an internal tail call elimination feature in other languages.

Example

For example, consider implementing $n!$.² Since $n!=n\ast (n-1)!$, we can continue to break down the factorial into smaller versions of itself. Our base case is when we reach $1!$:

int fact(int n) {
	if (n == 1)
		return 1;
	else
		return (n * fact(n - 1))
}

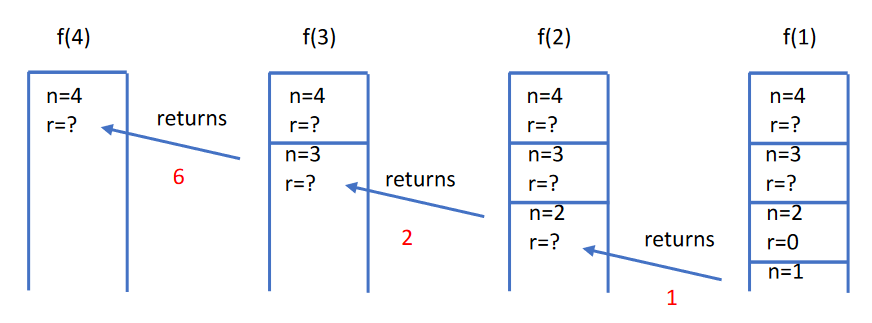
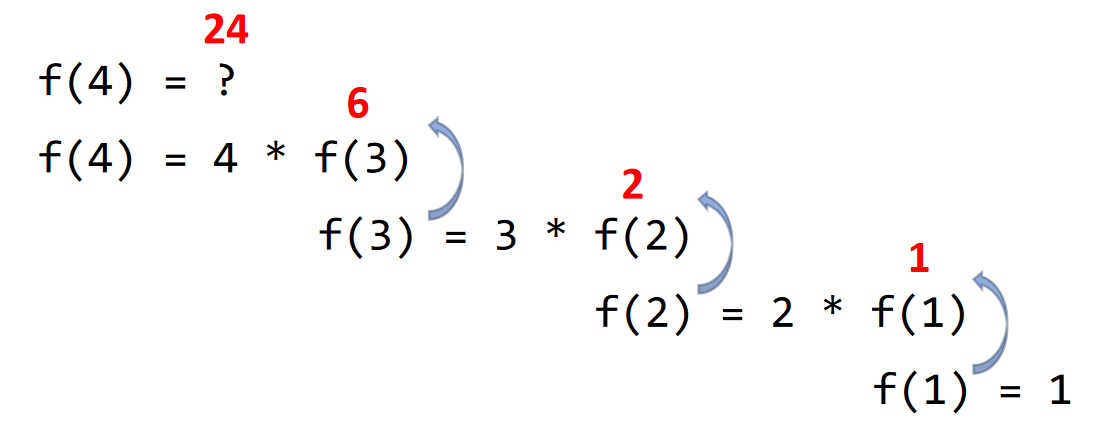On the stack, it looks something like this:

See also

• Backtracking

Footnotes

1. From Functional Programming in Python, by David Mertz. ↩

2. From Prof Stumm’s notes. ↩