Geometric optics

One of the main sub-fields of optics is geometric optics, where we approximate light waves as straight-line rays. We mainly use it when the size of the object is much bigger than the light’s wavelength. If that doesn’t hold (which does happen), or in complex phenomena like interference or diffraction, then we need to use wave optics.

Basics

There are two basic abstractions we use:

• Point source — single point that emits light rays in all directions.
  • It approximates a small light source in proximity.
  • Also approximates the focus of a laser beam, i.e., a laser beam focused to its tightest possible spot.
  • Bodies can be approximated as a collection of many point sources.
• Parallel rays (like the far-field approximation) — collection of parallel rays, mainly for distant objects.
  • Approximates a collimated (where its rays are made as parallel as possible) laser beam.

There are also two important parameters:

• Refractive index $n$ — property of transparent media that affects how much light ends at an interface.
  • We can assume air has a refractive index of 1.
• Optical path length (OPL) — is not the same as the physical length the light travels. It’s the length weighted by the refractive index.
  • In a homogeneous medium, we have a straight ray. Then, $\text{OPL}=nL$, where $L$ is length.
  • In an inhomogeneous medium, the light is unlikely to be straight, so we’d need to do a line integral. Then, $\text{OPL}={\int }_A^{B}n(s)ds$.

There are three fundamental laws of geometric optics:¹

• In a homogeneous medium, light travels in a straight line (rectilinear propagation).
  • By Fermat’s principle, in a homogeneous medium, the shortest path is trivially a straight line.
• Law of reflection — when a ray of light hits an interface dividing two optical media and reflects at the interface, the incident angle is equal to the reflective angle, ${\theta }_i={\theta }_r$. We define:
  • Incident angle ${\theta }_i$ — angle between ray and surface normal.
  • Reflective angle ${\theta }_r$ — angle between reflected ray and surface normal.
  • For a curved surface, we approximate with a small straight surface.
• Law of refraction (or Snell’s law) — when a ray of light hits an interface dividing two transparent media and refracts at the interface, the transmitted ray remains within the plain of incidence. Additionally, the sines of the angles wrt the surface normal are proportional to each other, i.e., $n_i\sin {\theta }_i=n_t\sin {\theta }_t$.
  • Transmitted angle ${\theta }_t$

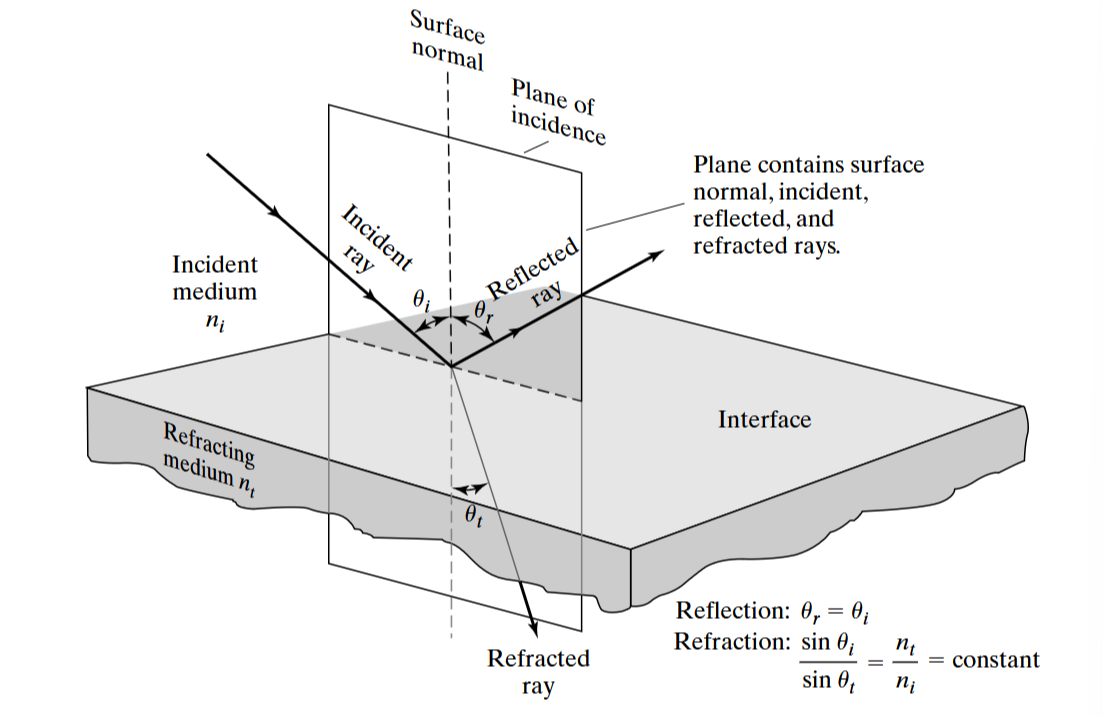
All three laws can be derived from Fermat’s principle, which states that light going from point A to point B will traverse the route with the shortest optical path length. Fermat’s principle also implies the principle of reversibility, i.e., for a route from A to B, if we reversed the path such that A was the source, it would take the same path.

Sub-pages

• Fundamental laws
  • Rectilinear propagation
  • Law of reflection
  • Snell’s law
• Fermat’s principle
• Optical imaging system
  • Gaussian formula
  • Thin lens
  • Spherical mirror
• Matrix optics

Footnotes

1. Image from Introduction to Optics, by Frank L. Pedrotti, Leno M. Pedrotti, and Leno S. Pedrotti. ↩