Law of reflection

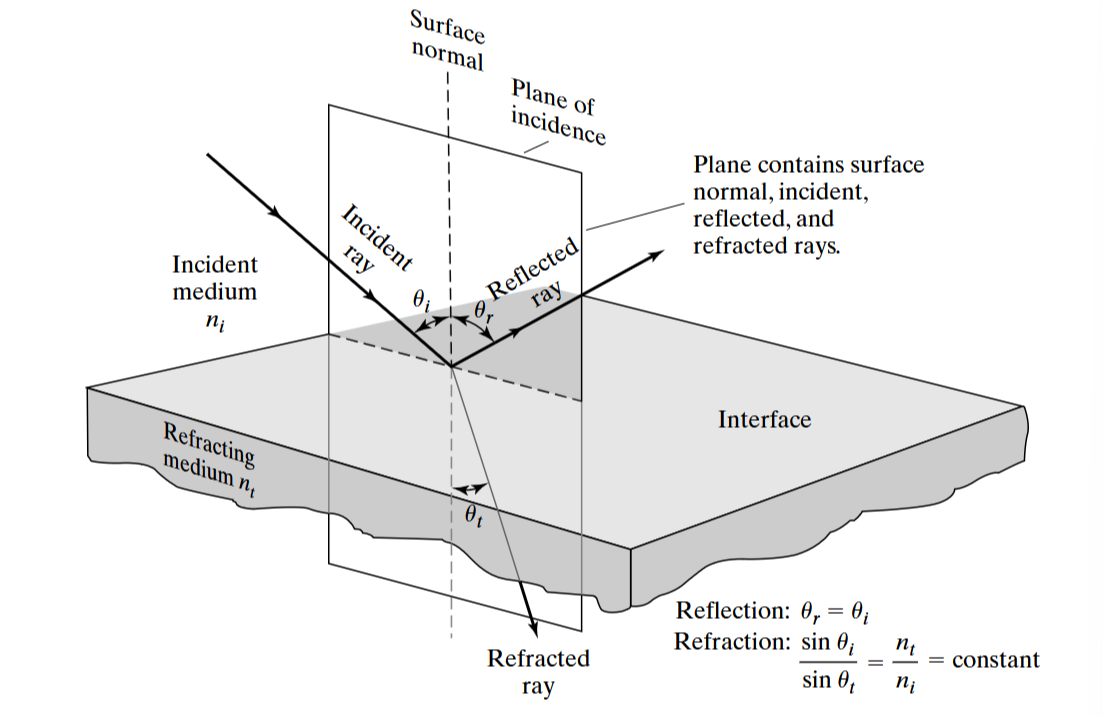
The law of reflection is one of the fundamental laws of geometric optics. It states that when a ray of light hits an interface dividing two optical media and reflects at the interface, the incident angle is equal to the reflective angle, ${\theta }_i={\theta }_r$.

We define ${\theta }_i$ as the incident angle (angle between ray and surface normal), ${\theta }_r$ as the reflected angle (angle between reflected ray and surface normal). For a curved surface, we can approximate with a small straight surface.

Derivation

We can derive the law of reflection with Fermat’s principle. 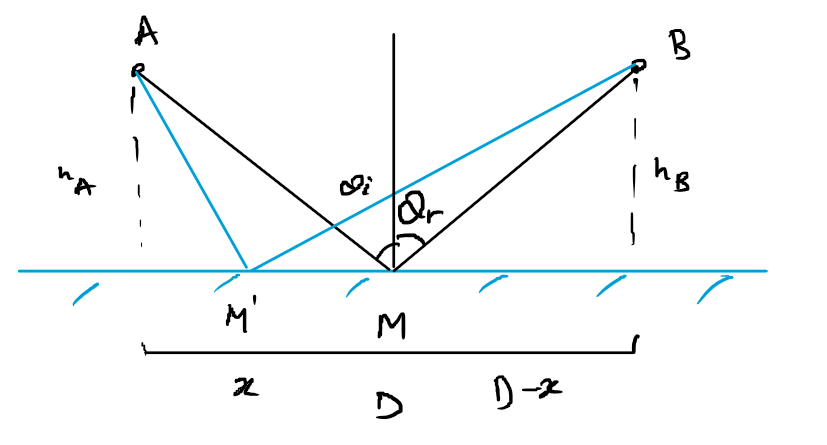We want to prove that given ${\text{OPL}}_{A\to B}=n(\overline{AM}+\overline{MB})$, this OPL formulation is the shortest.

\text{OPL} = n\left(\sqrt{h_A^2 + x^2} + \sqrt{h_B^2+(D-x)^2} \right) $$This is variable wrt $x$. Our job is to prove that it's minimised when $x = D-x$.

\frac{d\text{OPL}_{A\to B}}{dx}=0=n\left(\frac 12 \frac {2x}{\sqrt{h_A^2+x^2}}+\frac 12 \frac{2(D-x)}{\sqrt{h_B^2+(D-x)^2}}\right)

\frac{x}{\sqrt{h_A^2+x^2}}=\frac{D-x}{\sqrt{h_B^2+(D-x)^2}}

\frac{x}{\overline{AM}}=\frac{D-x}{\overline{BM}}

$$whichimpliesthat$$

\sin\theta_i=\sin\theta_r

\theta_i=\theta_r