Spherical mirror

concave:

• far away is upside down, real image
• close, where $d<f$, image is right side up and

convex:

• virtual image, right side up

concave case 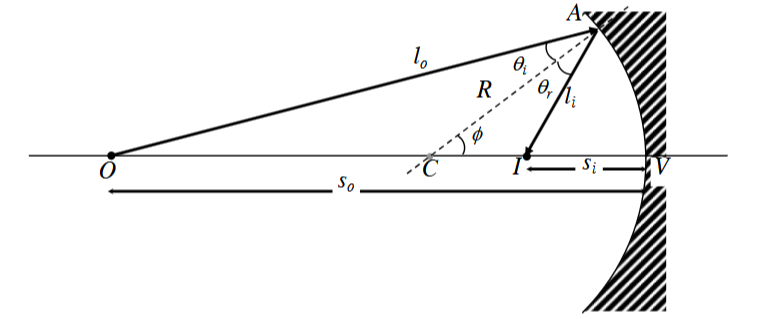reflective case, so we use Law of reflection similar to spherical refractive surface case, a spherical mirror can be considered as an OIS with the small angle approximation

same as Gaussian formula

$$\frac{1}{s_o}+\frac{1}{s_i}=\frac{1}{f}$$

where $f=\frac{R}{2}$.

sign convention:

• $O$ real, left of $V$ pos
• $V$ to right of $C$, then $R$ pos
• $I$ real, $I$ left of $V$
• $f>0$ for concave surface
• $f<0$ for convex surface
• real positive!

converging rays: real image even though image formed on the left rays can’t go to the right bc would be reflected but if rays are divergent, this causes virtual image

parallel rays coming in for focal length $f=f_1=f_2$ concave case

convex case image at infty

mirrors vs lenses

• mirrors
  • does not require transparent material
  • can be large
  • better structural support
• lenses
  • requires transparent material
  • difficult to be large
  • limited options for structural support
  • input/output occupy different spaces

example: Hubble Space Telescope

• why in space? because air is dense and scatters light. space is much more transparent. therefore less aberrations. higher light intensity
• rays hit primary mirror, reflected into a convex mirror, reflected through hole in primary mirror to an image sensor
• $R_1=12.75$ metres
• distance between mirrors is about 4.6 metres
• 

Angular resolution for stars 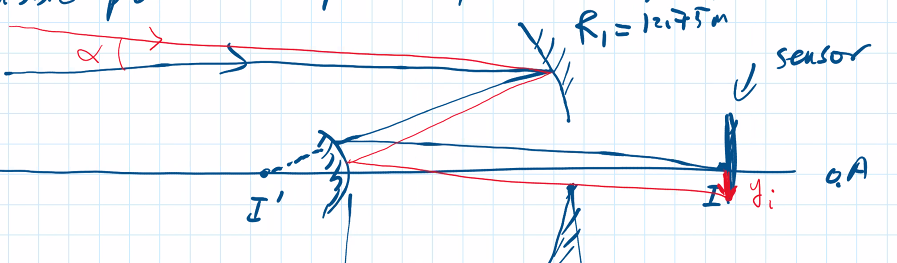need to find relationship between $\alpha$ and $y_i$

1. find imaging point of first mirror, which is basically the focus. if rays are roughly parallel $f_1=\frac{R_1}{2}=6.375$ metres since $f_1>d=4.6$ metres, then real image $I^{\prime }$ is serving as a virtual object for the 2nd mirror, bc light rays converge to second mirror (light rays going from RTL) 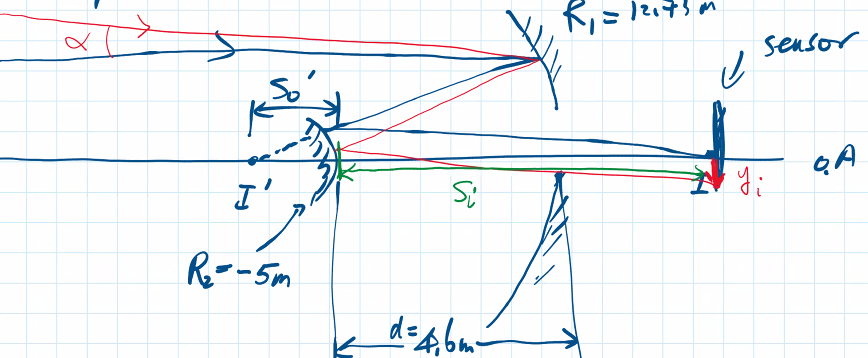$s_o^{\prime }=-(6.375-4.6)$ where radius of 2nd mirror is -5 m (negative bc convex)

$$\frac{1}{s_o^{\prime }}+\frac{1}{s_i}=\frac{1}{f_2}=\frac{2}{R_2}=\frac{2}{-5}$$

$s_i=6.12m$ $y_o^{\prime }=\alpha s_i^{\prime }$ find relation between $y_i,\alpha$ $y_i^{\prime }=y_o^{\prime \prime }=\alpha f_1$ $y_o/y_o^{\prime \prime }=M_{T_2}=-\frac{s_i}{s_o^{\prime }}$

$$y_i=-\frac{s_i}{s_o^{\prime \prime }}{y}_o^{\prime \prime }=-\frac{s_i}{s_o^{\prime \prime }}\alpha f_1=-\frac{6.12}{-(6.375-4.6)}\alpha \frac{R_1}{2}$$

= $22\alpha$ m/rad