Magnification

Optical imaging systems have the property of magnifying images. For OIS with transverse rotational symmetry (where if we look down the optical axis, the structure doesn’t change if it is rotated by an arbitrary angle wrt the OA), then we define:

• Transverse magnification $M_T$, which is the ratio of the image size on the image plane to the object size on the object plane.
  • Where the object plane and image plane are planes that are perpendicular to the optical axis at the object and image locations, respectively.
  • For example, if $M_T=2$, then the image is twice as large as the object in directions perpendicular to the OA (height and width).
  • A negative $M_T$ indicates the image is inverted.
• Longitudinal magnification $M_L$ is the ratio of image size along the OA to the object size along the OA. It relates how stretched or compressed the image is along the optical axis.
  • $M_L=M_T^2$, i.e., for changes in transverse magnification, the longitudinal magnification increases at a greater rate (i.e., depth is substantially increased).

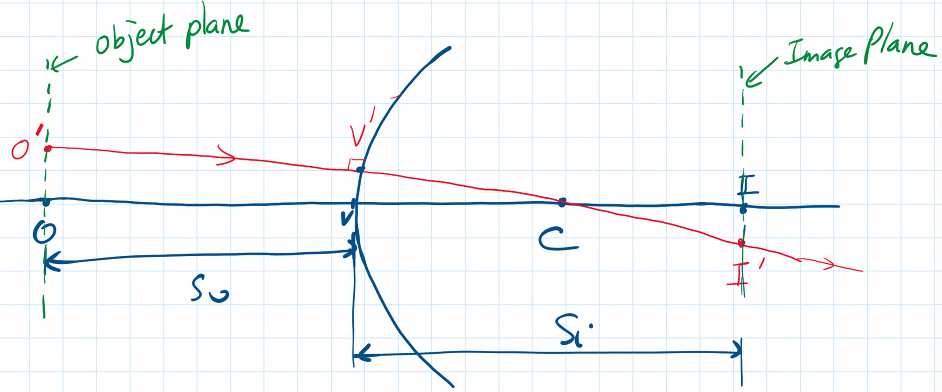
Transverse magnification

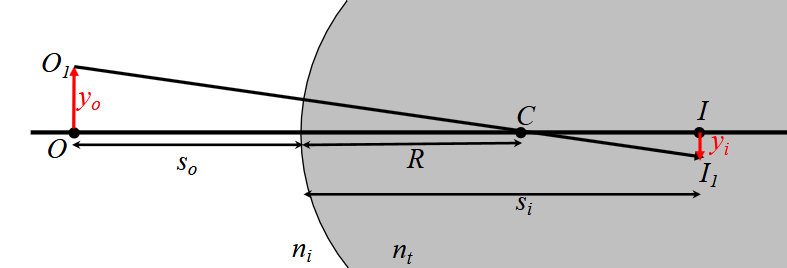The formula is given by (derived with triangles and the Gaussian formula):

$$M_T=\frac{y_i}{y_o}=-\frac{s_i-R}{s_o+R}=-\frac{n_i{s}_i}{n_t{s}_o}$$

i.e., in the case of a spherical surface, the image is inverted. For a thin lens and spherical mirror, the equation is the same for both:

$$M_T=\frac{y_i}{y_o}=-\frac{s_i}{s_o}$$

Note that for multiple lens systems, the total transverse magnification of the system is the product of the individual magnifications:

$$M_{T\text{sys}}=\prod M_{Ti}$$

Longitudinal magnification

The formula is given by (derived by differentiating the Gaussian formula):

$$M_L=\frac{d{s}_i}{d{s}_o}=-\frac{n_i{s}_i^2}{n_t{s}_o^2}$$

Note that in general $M_L\ne M_T$. The derivation for the above:

$$\frac{n_i}{s_o}+\frac{n_t}{s_i}=\frac{n_t-n_i}{R}$$ $$-\frac{n_i}{s_o^2}-\frac{n_t}{s_i^2}\frac{d{s}_i}{d{s}_o}=0$$

For a thin lens and spherical mirror:

$$M_L=\frac{d{s}_i}{d{s}_o}=-\frac{s_i^2}{s_o^2}$$