Thin lens

In geometric optics, thin lenses are a useful approximation for sufficiently thin optical devices. There are two main types of thin lenses of note.

• Convex lenses have a thick central region and thin edges.¹ They converge incoming light rays.
• Concave lenses have a thin central region and thick edges. They diverge incoming light rays.

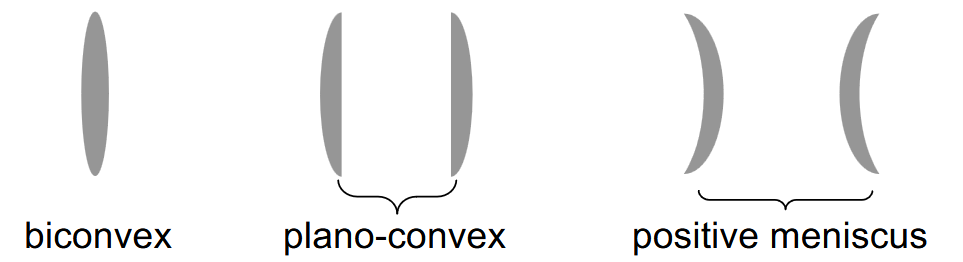
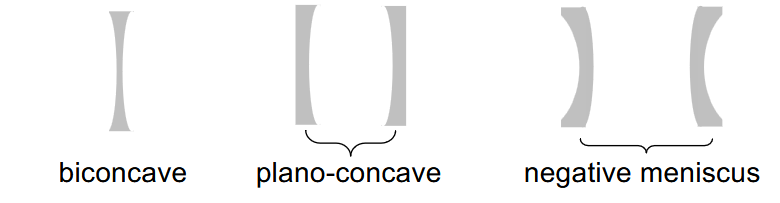
Sign convention

As usual, we keep a very specific sign convention:

• Focal length $f$
  • Positive for converging lenses (convex).
  • Negative for diverging lenses (concave).
• $R$ is positive if the centre of curvature lies to the right of the surface. Negative if the centre of curvature is to the left of the surface.

In general, convex lenses can create real and virtual images from real objects. Concave lenses can create only real images from real objects.

Calculations

The Lensmakers’ formula gives us a useful relation for thin lens and spherical mirrors. Note the terms without $n$ assume an ambient medium of air.

$$\frac{1}{s_o}+\frac{1}{s_i}=\frac{1}{f}=\frac{n_l-n_m}{n_m}\left(\frac{1}{R_1}-\frac{1}{R_2}\right)$$

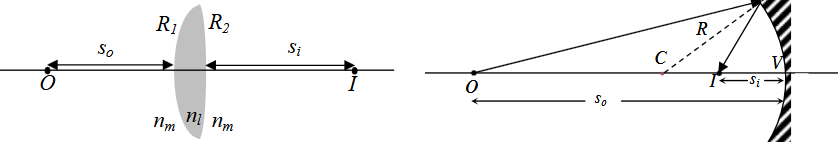Reversibility implies that we can swap $s_o$ and $s_i$ and still get a proper image. The magnification may be a different magnitude.

If our lens consists of multiple refracting surfaces, we need multiple steps in our analysis. Some notes:

• Be careful what we define as $s_i$ and $s_o$. It is reserved for the systemwide object/image locations.
  • For constituent parts, we should ideally define an $s_i^{\prime }$ or $s_o^{\prime }$ where necessary.
• Note that the output of one lens will act as the input to the next lens.
  • For example, if our first lens outputs converging rays (for a virtual image), the second lens will treat it as a virtual object.
  • And for an output $I^{\prime }$ from first surface, this is the same as $O^{\prime \prime }$ for the second surface!
• For a two-step lens, we can do: equation 1 + equation 2.

Lensmaker’s formula 1/R_1 - 1/R_2 positive if R_1 > 0 and R_2 < 0

thin lens in a symmetric medium in air, $f_o=f_i=f$. so for a lens, we just get one focal length! Gaussian formula for thin lens

special case relevant for eyes. optimal distance for corrective lenses is at d = f_2. transverse magnification may be different for eyes

Footnotes

1. From ECE318 — Fundamentals of Optics lecture slides. ↩