ALOHA

ALOHA is a computer networking system that is a random access protocol for multiple access channels. The core idea is that collisions are allowed to happen, and then recovered via re-transmission.

In slotted ALOHA, time is discretised and frames can only be transmitted only at the beginning of a time slot. All slots are the same size. Nodes are synchronised. If nodes transmit concurrently in a single slot, the collision is detected by all nodes. When node has a new frame to send, it transmits in the next slot. With no collision, we have a success! But with a collision, each node will retransmit the frame in each subsequent slow with a probability $p$ until success. This allows a probabilistic avoidance of conflicts (much like Raft election timeouts). 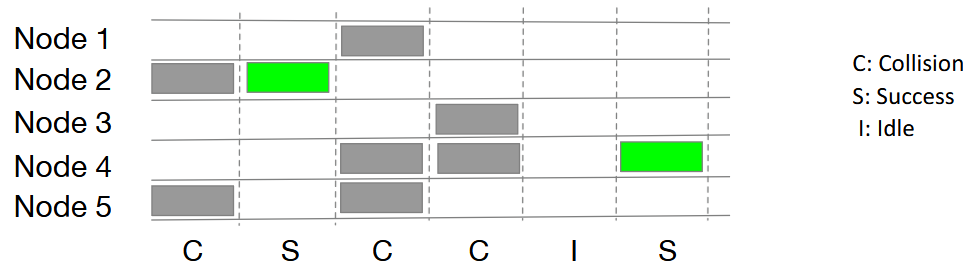In pure ALOHA, time is continuous and frames can be transmitted starting at any point in the timeline. This is much simpler and doesn’t require clock synchronisation. However, the collision probability increases, since there’s a higher possibility of frame overlaps.

Analysis

There are some obvious pros and cons that come from this implementation:

• Pros
  • A single active node can continuously transmit at the full rate of the channel.
  • It is highly decentralised. The only things that need to be in sync are the time slots in each node.
  • It’s also simple!
• Cons
  • Collisions waste slots.
  • Slots can be idle.
  • Nodes may be able to detect collision in less than the time to transmit a packet.
  • Clock synchronisation.

Efficiency

The efficiency is defined as the long-run fraction of successful slots in a system where there are many nodes, all with many frames to send. With $N$ nodes and a transmission probability of $p$, the max efficiency is $0.37$, i.e., useful transmissions occur in the channel at most 37% of the time!

The probability of successful transmissions in a timeslot is given by a binomial distribution, where $X$ is the number of packets attempted for re-transmission.

$$P(X=k)=\left(\genfrac{}{}{0ex}{}{N}{k}\right)p^k(1-p{)}^{N-k}$$

i.e., for an idle slot, $k=0$. For a successful slot, $k=1$. For a collision slot, $k\ge 2$.

The probability that a given node has a success in a slot is:

$$P_s=p(1-p{)}^{N-1}$$

On average, the time to success is geometrically distributed with parameter $P_s$. Hence the time to success is $1/P_s$.

For find the $p$ that maximises $P(X=1)$, we take the derivative, which gives us that $p^{\ast }=\frac{1}{N}$. For many nodes, we then take the limit:

$$\underset{N\to \infty }{\lim }N{p}^{\ast }(1-p^{\ast }{)}^{N-1}=\frac{1}{e}\approx 0.37$$

For pure ALOHA, the efficiency is 0.18. Even worse!