Binomial distribution

The binomial distribution is a probability mass function that generalises the Bernoulli distribution for $n$ trials if:

If $I_{j}$ is the indicator function for an event $A$ in trial $j$ , then:

X = I_{1} + I_{2} + \dots + I_{n}

i.e., $X$ is the sum of Bernoulli random variables associated with each of the $n$ independent trials.

We denote it with:

X \sim B (n, p)

where $X \in [0, n]$ , a discrete random variable.

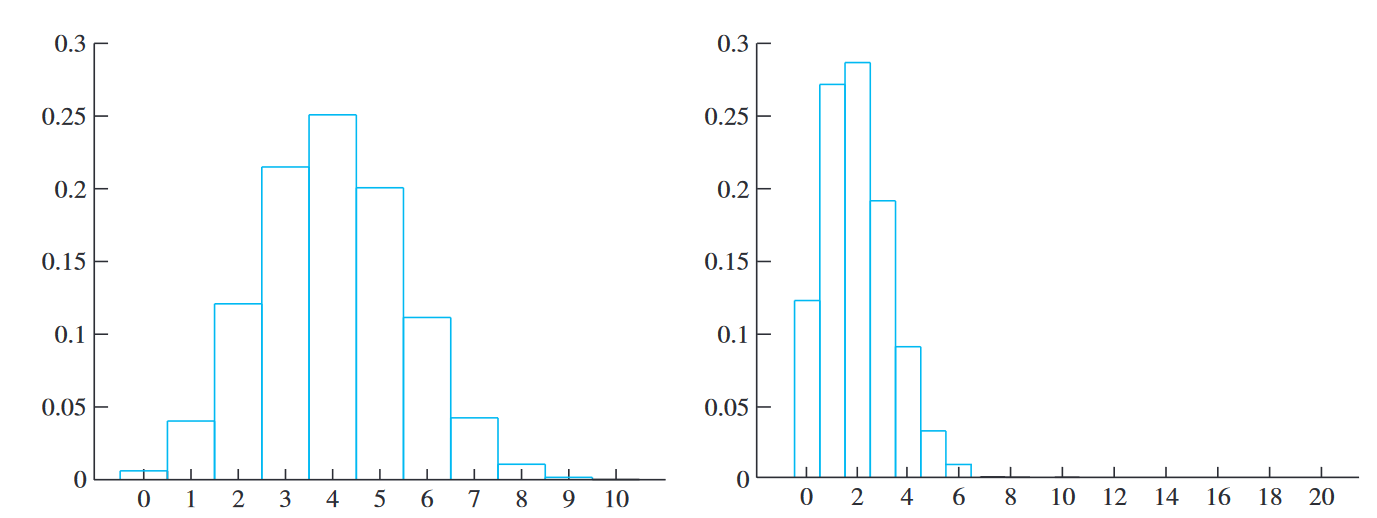
For example, below are the distributions for $B (10, 0.4)$ and $B (20, 0.1)$ .¹

Computations

The probability mass function of $X$ is given by:

P (X = k) = {(k n) p^{k} (1 - p)^{n - k} 0 for k \in [0, n] otherwise

The mean and variance are given by:

μ_{X} = n p

σ_{X}^{2} = n p (1 - p)

The binomial probability law gives us the probability for exactly $k$ successes in $n$ independent Bernoulli trials, where $k \in [0, n]$ .

p_{n} (k) = (k n) p^{k} (1 - p)^{n - k}

We extend this with a form of the binomial theorem, in cases where we want the probability of at least $k$ successes in $n$ trials:

p = k = k_{0} \sum n (k n) p^{k} (1 - p)^{n - k}