Angular resolution

The angular resolution of an optical sensor is the smallest angular separation of two points that can be resolved by the sensor. If the angle subtended by an object is less than the angular resolution, then the sensor can’t resolve the information (multiple points map to a single “pixel”). For the human eye, the angular resolution is about 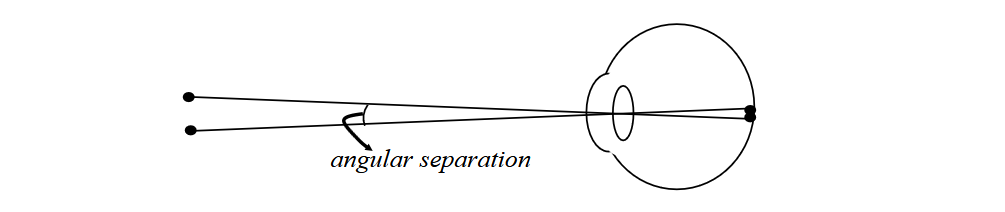$300\mu \text{rad}$. The resulting angle from an object of size $y_0$ at distance $D$ for an unaided eye is:

$${\alpha }_{\text{unaided}}=\frac{y_0}{D}$$

When we look through a magnifying glass (a convex lens), the resulting virtual image formed by the magnifying glass can have a much larger resulting angle at the eye than the unaided angle. As a result, it produces a much larger real image at the retina.

$${\alpha }_{\text{mag}}=\frac{y_i}{-s_i}=\frac{y_o}{s_o}$$

We define the magnifying power (MP) as the ratio of the magnified angle to the unaided angle. Note that the MP is different from the transverse magnification.

$$\text{MP}=\frac{{\alpha }_{\text{mag}}}{{\alpha }_{\text{unaided}}}$$

Construction

Suppose we have the eye: 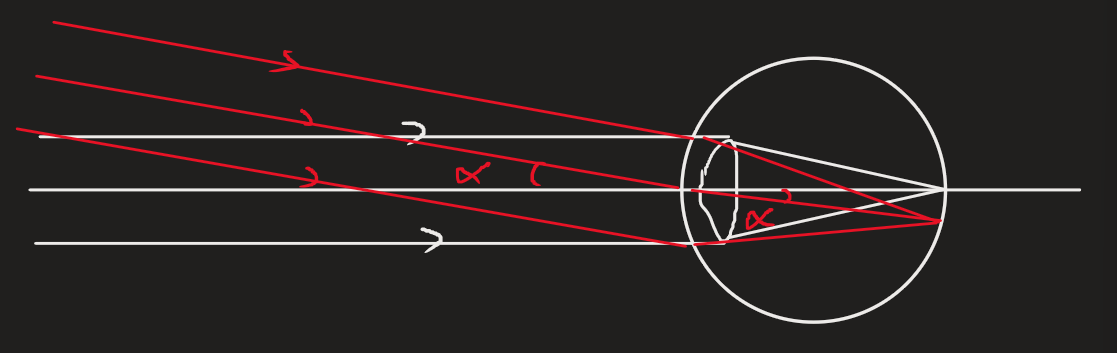Note that the ray passing through the optical centre has the same angle $\alpha$. If the two points fall on two different photoreceptive cells, then they can be resolved by the sensor (our retina). Otherwise, we can’t resolve it.

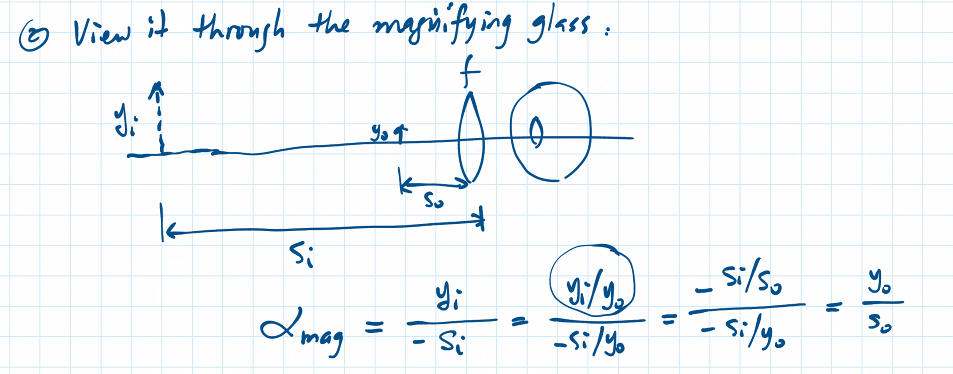
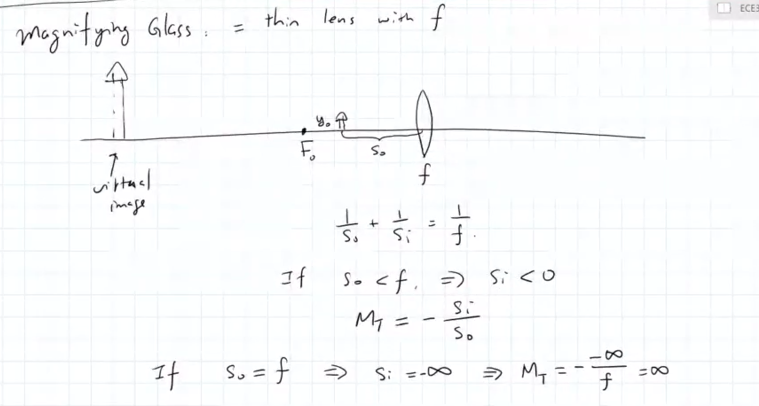
magnifying glass:

• MT = -s_i/s_o
• when s_o = f, then s_i ⇒ infty
• M_T → infty

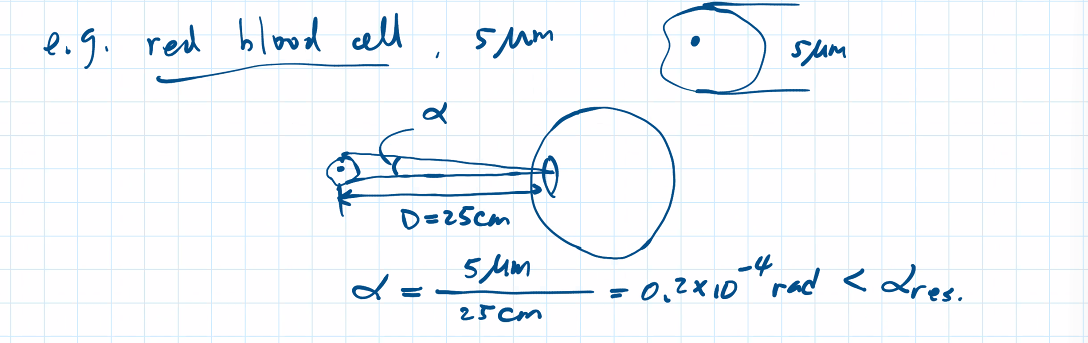
however, we still can’t see a red blood cell. it’s not the size of the object (or size of the image), but the angle subtended by the object that matters! ${\alpha }_{\text{mag}}=\frac{y_i}{-s_i}$

$$=\frac{\frac{y_i}{y_o}}{\frac{-s_i}{y_0}}$$

=(-s_i/s_o)/(-s_i/y_o) = y_o/s_o

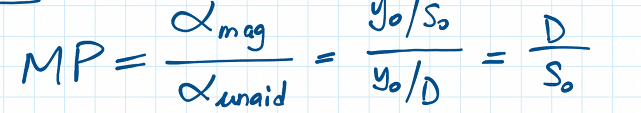
s_o == distance from magnifying glass define: magnifying power $\ne$ transverse magnification case 1: viewing object @ infty case 2: viewing obj @ D two extremes image in between these two distances == case 1 < MP < case 2